skanuj0021 (194)

1

2

3

4

6

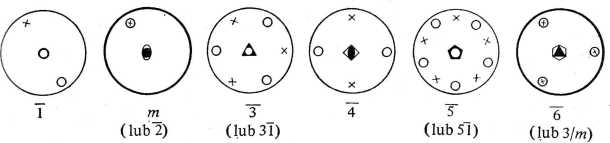
Rys. 1.9. Rzuty stereograficzne punktów związanych symetrią osi zwykłych i inwersyjnych

znajdują się na półkuli N czy S. Przecięcia prostych z płaszczyzną równikową (płaszczyzną rzutu) wyznaczają bieguny stereograficzne (rys. 1.8). W płaszczyźnie rzutu, wewnątrz koła rzutu, krzyżyk ( x ) oznacza rzut stereograficzny punktu znajdującego się na półkuli N, natomiast kółko (o) — rzut stereograficzny punktu z półkuli S. Na rysunku 1.9 przed stawiono rzuty stereograficzne zbiorów punktów równoważnych wykazujących symetrię zwykłych i inwersyjnych osi symetrii, które omówimy w dalszym tekście. Każdy z nich otrzymuje się stosując operację symetrii do punktu początkowego i powtarzając operację tyle razy, ile jest potrzebne, by nie otrzymać już żadnego nowego punktu. Konstruując w ten sposób zbiory punktów odpowiadające różnym operacjom symetrii stwierdza się, że pewne operacje określane różnymi nazwami są w rzeczywistości identyczne.

1.1.4. Identyczność operacji symetrii

Wykorzystując operatory lub rzuty stereograficzne punktów równoważnych (rys. 1.9) można udowodnić prawdziwość następujących tożsamości:

l = 2 = c

2=1 sm

3 = 6 = 31 (oś 3 plus środek symetrii 1)

4e4

5sl0s5l

6 = 3 = 3/m (Xjm oznacza oś X prostopadłą do płaszczyzny m)

TÓs 5 s 5/m

Ostatecznie jako elementy symetrii pozostają tylko

1 2 3 4 5 6...

T m 3 4 5 6 ...

25