skanuj0028 (74)

Transkodery można zrealizować w postaci układu (rys. 4.399a) złożonego z dekodera (zmieniającego kod wejściowy X na kod pierścieniowy) i enkodera (zmieniającego kod pierścieniowy uzyskany na wyjściach dekodera na żądany kod wyjściowy Y). Rozwiązanie takie nie jest zazwyczaj optymalne, gdyż nie uwzględnia możliwości wielokrotnego wykorzystania niektórych funkcji logicznych. Są jednak przy-

Transkoder

Rys. 4.399. Schematy ideowe transkoderów

a) zbudowanego z enkodera i dekodera, b) zbudowanego w postaci wielowyjściowego układu kombinacyjnego

padki, gdy takie rozwiązanie jest korzystne. Mają one miejsce wówczas, gdy zarówno wymagany dekoder, jak i enkoder, albo przynajmniej jeden z nich, są dostępne w postaci scalonej.

Jeśli zarówno dekoder, jak i enkoder nie są dostępne w postaci układów scalonych, to lepsze rozwiązanie można uzyskać w wyniku syntezy transkodera jako wielowyjściowego układu kombinacyjnego (rys. 4.399b).

Przykłady syntezy i rozwiązań transkoderów

Przykład 1. Zaprojektować transkoder służący do przetwarzania kodu BCD 8421 na kod BCD 2*421.

W celu zaprojektowania takiego transkodera należy przedstawić rozpatrywane kody w tablicy (rys. 4.400a). Tablica kodów stanowi

a

£> \BA

nc\oo 01 11 w

	D 8	c 4	B 2	A 1	D' 2	C' 4	B' 2	A' 1
0	0	0	0	0	0	0	0	0
1	0	0	0	7	0	0	0	1
2	0	0	1	0	0	0	1	0
3	0	0	1	1	0	0	1	1
4	0	1	0	0	0	1	0	0
5	0	1	0	1	0	1	0	1
6	0	1	1	0	0	1	1	0
7	0	1	1	1	0	1	1	1
8	1	0	0	0	1	1	1	0
9	1	0	0	1	1	1	1	1

0	0	1	1
0	0	1	1
1	1

c

A >-

^£^l>

\BA nc\	00	C' 01	11	10
00	0	0	0	0
01	1	1	1	1
11
10	1	1

A'

B'

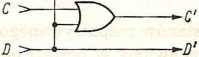
Rys. 4.400. Transkoder kodu BCD 8421 na kod BCD 2*421

a) tablica rozpatrywanych kodów, b) tablice Karnaugha, c) schemat logiczny

381