skanuj0114 (23)

208 B. Cieślar

Rys. 5.6.1

<*=-45°

Rys. 5.6.2

M=75V2kNm

Z równań (1) i (2) obliczamy M_x i M_y.

M_x = 75 kNm;

M_y = -75 kNm.

Wartość momentu zginającego:

M = i/(75)² +(-75)² =75^2 kNm.

Położenie wektora M:

tg (p = -1;    ->    q> = -45° +n-180°;

sin cp =    ->    9 = -45° +n-360°,

czyli <p = -45° + n-360°.

Położenie wektora „M” pokazano na rys. 5.6.2.

pionowo równomiernie rozłożo

Pozioma belka (rys. 5.7.1) jest obciążona

nym obciążeniem „q” oraz poziomą siłą „P”, przyłożoną w połowie rozpiętości. Zaprojektować prostokątny przekrój poprzeczny belki, jeżeli: q = 6 kN/m, P = 18 kN, I = 3 m, f_d = 15 MPa, h/b = 2.

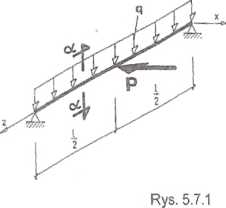
Rozwiązanie

Jeżeli do belki przyłożymy tylko obciążenie „q”, to spowoduje ono powstanie momentów „M_x” o rozkładzie pokazanym na rys. 5.7.2a. Jeżeli następnie przyłożymy do belki tylko siłę „P”, to spowoduje ona powstanie momentów zginających „My”, o rozkładzie przedstawionym na rys. 5.7.2b. Sytuując wektory „M_x" i „M_y" na przekroju (rys. 5.7.2c) łatwo zauważyć, iż są one składowymi wektora „M” w układzie osi głównych, centralnych (x, y). Funkcja naprężeń, zbudowana na potrzeby niniejszego zadania, będzie zatem mieć poniższą postać:

^Jx    ^Jy

Największe naprężenia normalne wystąpią w punktach przekroju najbardziej odległych od linii obojętnej. Będą to punkty I i II, przy czym:|a,| = |ct„|, więc:

_ |M_x|0,5h jM_y|0,5b

®max    j '    •

^Jx    ^Jy

W połowie rozpiętości belki momenty „M_x“ i „My” są największe i ich wartości podstawiamy do powyższego wzoru (por. zad. 5.5):

dp    pi

8 ^0|Sh , T°-^5b _<f tit ^d>

12 12

Po podstawieniu danych liczbowych otrzymamy rozwiązanie: h £ 0,3 m.

Przyjmujemy:

h = 30 cm;    b = 0,5h =15 cm.

Dla tak przyjętych wymiarów o_max =15 MPa.