46937 skanuj0045 (23)

70 B. Cieślar

Rozwiązanie

Z równań równowag! wyznaczamy oddziaływania podpór (rys. 2.21 .b).

£M_a=0; -S₃-6 = 0;    (1)

£P_Z=0;    S₂cosa - Pcosa = 0; S₂ = 60kN;    (2)

^P_y = 0;    S, + S₃ +S₂ sina- Psina = 0; S, = 0.    (3)

Obliczamy zmiany długości prętów:

*•1 =

^S2*2-    6Q1Q~³ -5

EF 2-10⁵-10-10“

^x'^3=_ef^ł=o;

= 0,0015 m.

Ponieważ pręty 1 i 3 nie zmieniły długości, więc przesunięcie pionowe punktu A równe jest zeru - ua_y = 0.

Przesunięcie poziome punktu A, jak wynika to z zależności geometrycznych z rys. 2.21.1b, będzie równe:

Uax = Ua = J^ ₌ _^0,0°¹⁵ n0,0025 m = 2,5 mm. cosa 0,6

2.22.

Żelbetowa płyta zawieszona jest na dwóch stalowych linach (rys. 2.22.1 a)

składających się z 20 strun, o średnicy 2 mm każda. Sprawdzić naprężenia w linach, jeżeli długość liny I = 5 m, ciężar płyty G = 15 kN, a wytrzymałość obliczeniowa fd = 215 MPa.

Rozwiązanie

Z równania równowagi (rys. 2.22.1 b)

£P_Z=0;    -G + R = 0; R = G.

Z równań równowagi dla węzła C (rys. 2.22.1c) mamy: £P_Z=0; S, = S₂;

£P_y = 0;    R - 2Ssin(p=0.

Pole przekroju liny

= 62,832 mm².

F = 20^^-4

Naprężenie w linie: ,

= 198,94 MPa.

Sj_ q _    15,0 • 10"³

F ” 2sina • F 2 • 0,6 ■ 62,832 ■ 10^-1

A zatem:

o = 198,94 MPa < f_d = 215 MPa.

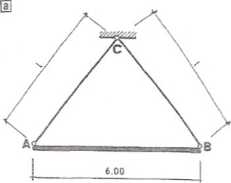
Rys. 2.22.1

2.23.

Stalowe szyny (rys. 2.23.1) o długości I = 8 m były układane w tempera

turze 10 C. Jak duża musi być przerwa (A) między nimi, aby w szynach nie powstały naprężenia po ogrzaniu o 50 K? Jak duże powstałyby naprężenia w szynach, gdyby przerw nie było? Do obliczeń przyjąć: cc* = 1,25-10‘⁵/ °K, E = 2'10⁵ MPa. Rozwiązanie

Niezbędną długość szczeliny obliczymy ze wzoru:

A = a,At • I = 1,25-10'⁵-50-8 = 0,005 m = 5 mm.

W przypadku braku przerw (szyna jest nieskończenie długa), całkowita zmiana długości szyny Al = 0; a zatem:

Al = AI(At)+Al(R) = a_tAH+H =0;

gdzie R - siła osiowa w szynie.