15452 skanuj0158 (14)

296 B. Cieślar

Rozwiązanie

Obliczamy współczynniki równania sekularnego:

51    = 90,

5₂    = 0,

5₃    = 0.

Równanie sekularne przyjmuje postać: c³ - 90 a² = 0; a² (a - 90) *= 0,

a stąd naprężenia główne mają wartość: d = 90 MPa, 02 = a₃ = 0.

W analizowanym punkcie mamy jednoosiowy stan naprężenia.

Wyznaczamy cosinusy kierunkowe osi naprężeń głównych, d w 90 MPa;

(30 - 90)h + 30mi + 30ni = 0;

30li + (30 - 90)mi + 20ni = 0;

3011    + 301TH + (30 - 90)ni » 0;

(h)² + (mi)² + (ni)² = 1,

a stąd

Ił = mi = m = ±^; a = 54,74°,

czyli oś naprężenia głównego 01 jest nachylona pod takim samym kątem do dodatnich półosi x,y,z (rys. 7.15.2). o₂ - 0;

(30 - 0)l₂ ⁺ 30m₂ + 30n₂ ⁼ 0;

301₂    + (30 - 0)m₂ + 20n₂ ⁼ 0;

30l₂ + 30m₂ + (30 - 0)n₂ ⁼ 0;

(b)² + (m₂)² + (n₂)² = 1.

Ponieważ trzy pierwsze równania są liniowo zależne, więc układ redukuje się do dwóch równań o trzech niewiadomych. Nie ma zatem jednoznacznego rozwiązania.

identyczny wynik otrzymamy dla cosinusów kierunkowych naprężenia a₃ = 0. Z fizycznego sensu zagadnienia wynika, iż każda oś leżąca w płaszczyźnie prostopadłej do kierunku naprężenia ai jest osią naprężenia głównego a₂ = o₃.

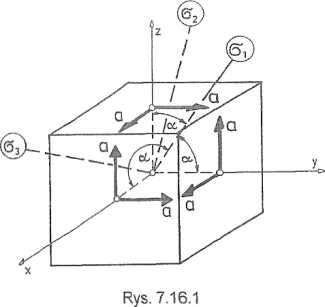
Dane są składowe stanu naprężenia w punkcie (rys. 7.16.1):

a_x = 0, c_y = 0, a_z = 0, ixy = txz = x_yz = a, gdzie a > 0 w MPa. Należy wyznaczyć wartości i kierunki naprężeń głównych.

Rozwiązanie

Współczynniki równania wiekowego:

Si = 0, S₂ = - 3a², S₃ = 2a³. Równanie wiekowe przyjmuje postać:

a³ - 3a ct - 2a = 0.

Obliczamy pierwiastki tego równania.

P = 0;

o_H = [-3(-3a²)]^1/2 = 3a;

COS3(p = --'    = 1;

2(3a)

<p = 0.

Stąd: k = 1;

en = ^3a cos(O) = 2a;

k = 2;

ct2 = ^3a cos(^tc 1 - O) = - a;

k = 3;

<J3 = ^3a cos(|it 2 - O) = - a.

O    O

Obliczamy cosinusy kierunkowe osi naprężeń głównych, ai = 2a;

(0 - 2a)h + a mi + a ni = 0; a li + (0 - 2a)mi + a ni = 0; a h + a mi + (0 - 2a)ni = 0;

(li)² + (mi)² + (m)² = 1,