skanuj0145 (14)

270 B. Cieślar

Naprężenie styczne:

5,185 MPa.

T_aS_x, ₌ Q,36 • 0,2 • 0,08 • 0,14 J_x.b 0,0007776-0,2

Ponieważ wektory naprężeń normalnych są tutaj współliniowe, więc możemy je zsumować algebraicznie:

o = o(N) + a(M) * 6,667 + 30,864 = 37,531 MPa.

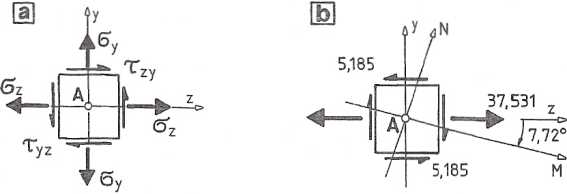
Do określenia składowych stanu naprężenia w punkcie A przyjęto prostokątny układ współrzędnych o osi „z” równoległej do osi podłużnej belki i osi „x” prostopadłej do płaszczyzny bocznej belki (rys. 7.1.2b).

Ponieważ płaszczyzna boczna belki jest nieobciążona, to:

Ox ⁼ t_Xy ^s Txz “ 0,

a przyjmując, iż tzw. wzajemny docisk włókien można pominąć mamy:

Oy = 0.

Po porównaniu rzeczywistych zwrotów naprężeń oixz umownie dodatnimi ich kierunkami w przyjętym układzie odniesienia (por. rys. MO) mamy:

oz = 37,531 MPa,    m - 5,185 MPa.

Tym samym określiliśmy wszystkie składowe stanu naprężenia w punkcie A. Ponieważ towarzyszące naprężeniu normalnemu o naprężenia styczne są równe zeru, jest ono zatem naprężeniem głównym. Pozostałe dwa kierunki leżą w płaszczyźnie (z,y) i ich położenie określa kąt a:

2(-5,185)

37,531-0

0,2763,

2t

tan2a =-?—

o_z-o_y

a = - 7,72° + n-90°, gdzie n = 0,1,2,

Wartości naprężeń głównych obliczone za pomocą wzoru (I-7) z rozdz.l, wynoszą: om = 38,234 MPa, on = - 0,703 MPa.

Rys. 7.1.3

VII. Stan naprężenia, stan odkształcenia    _ 271

Ostatecznie:

ci * 38,234 MPa, a₂ = 0, o₃ = - 0,703 MPa.

Wyniki pokazano na rys. 7.1.3b.

Przekrój poprzeczny a-a belki (rys. 7.2.1) obciążony jest siłami wewnętrznymi: M_a - - 600 kNm, T„ = 1800 kN, N_a = 2400 kN. Wyznaczyć wartości i kierunki naprężeń głównych w punkcie A przekroju.

Rozwiązanie

W celu określenia składowych stanu naprężenia przyjmujemy kartezjański układ współrzędnych, pokazany na rys. 7.2.2.

■?

|^| 16 cm U|

Ponieważ powierzchnia belki w punkcie A jest nieobciążona, to a_x = 0, % = 0 oraz txz = 0. Zakładając, że wzajemny docisk włókien można pominąć, to a_y = 0. Pozostałe składowe stanu naprężenia zależą od sił wewnętrznych, których działanie na przekrój pokazano na rys. 7.2.3a, a naprężenia spowodowane nimi na rys. 7.2.3b.

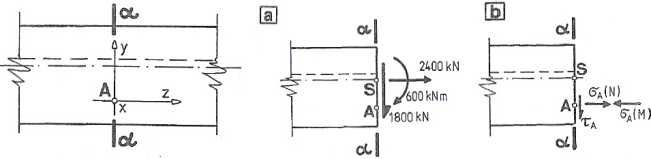
Rys. 7.2.2

Rys. 7.2.3