85108 skanuj0157 (14)

294

B. Cieślar

7.14 13 Dane są składowe stanu naprężenia w punkcie: o_x = O, o_y = 0, o_z = 0,

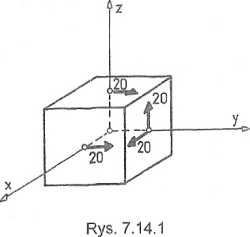
Txy = 20 MPa, T*z = 0 MPa, rzx - 20 MPa. Należy wyznaczyć wartości i kierunki naprężeń głównych.

Rozwiązanie

Na rys. 7.14.1 przedstawiono składowe stanu naprężenia. Obliczamy wartości niezmienników stanu naprężenia:

51    =0,

5₂    = - 800,

S₃=0.

Równanie sekulame przyjmuje postać:

o³ - 800 o = 0;

- 800) = 0.

Wartości naprężeń głównych są więc równe:

01    = 20 V2 MPa,

02    “ 0,

o₃ = -20 V2MPa.

Wyznaczamy cosinusy kierunkowe poszczególnych osi naprężeń głównych z układu równań (I-5 - rozdz.l):

01    = 20-72 MPa, - (h, mi, m);

(0-20V2)li + 20mi =0;

20h+ (0 - 20 V2 )mi + 20m = 0;

20mi + (0 - 20-v/2 )m = 0;

(li)²+(mi)² + (ni)² = 1,

stąd

h=±|; ^mi =±    m=i.

0₂    = 0, - (t, m_2l n₂);

20 m₂ = 0;

201₂ + 20 n₂ = 0;

20 m₂ = 0;

(I2 )²+ (m₂)² + (n₂)² = 1,

stąd

k m₂'= 0; n₂= ±—. a₃ = - 20 V2 MPa, - (l₃, m_3l n₃);

stąd

20>/2I₃ + 20 m₃ = 0;

201₃ + 20 -\/2 m₃ + 20 n₃ = 0; 20 m₃ + 20 V2 n₃ = 0;

(l3)²⁺ (m₃)² + (n₃)² = 1, | f +^; m₃ = ±^; n₃ = +1

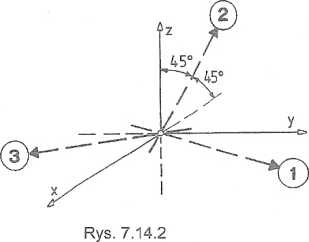
Na rys. 7.14.2 pokazano położenie kierunków naprężeń głównych.

7.15.

Dane są składowe stanu naprężenia (rys. 7.15.1):

o_x - 30 MPa,    a_y - 30 MPa, a_z = 30 MPa,

Txy = 30 MPa,    t_xz = 30 MPa, x_yz ⁼ 30 MPa.

Należy wyznaczyć wartości i kierunki naprężeń głównych.