skanuj0081 (30)

142 B. Cieślar

45.3. Oddziaływania podpór (rys. 4.5.3a): £M_a=0; P₁3 + P₂10-V_b6 = 0; £M_b = 0; -P₁3+P₂4+V_a6=0.

Stad:

V_A = 23,33 kN, V_B = 46,67 kN.

4-54. Funkcje sił wewnętrznych Przedział I - z e (0;3),

M(z)= V_A z= 23,33z;

M(0)= 0; M(3)= 70 kNm;

T(z)= V_A S 23,33 kN.

Przedział II - z e (3;6),

M(z)= V_A z - Pi (z-3)= 23,33z - 60(z-3);

M(3)= 70 kNm; M(6)= -40 kNm;

T(z)= V_A - Pt = 23,33 - 60= -37,67 kN.

Przedział III - z e (0;4),

M(z)= -P₂ z = -10z;

M(0)= 0; M(4)= -40 kNm;

T(z)= P₂ = 10 kN.

Wykresy sił wewnętrznych pokazano na rys. 4.5.3.

4.5.5. Projektowanie przekroju poprzecznego belki

podobnie jak w poprzednim przykładzie, projektowanie musimy przeprowadzić dla największego momentu dodatniego i największego momentu ujemnego.

M - +70 kNm:

_ 70 -10~³ 4,75a ^r 55,25a⁴

<60;

(D

a > 0,0465 m;

(2)

70 • 10"³ - 2,25a ^ 2_Q. 55,25a⁴

a £ 0,0456 m.

M = -40 kNm:

_q = -⁴-⁰ '-¹-⁰^'    < go;    (3)

^f 55,25a⁴

a £0,0301 m;

a £0,0486 m.

Nierówności (1),(2),(3) i (4) będą więc spełnione dla a > 4,86 cm. Przyjmując a = 5 cm, otrzymamy wartości naprężeń przedstawione na rys. 4.5.2b.

40-10~³-4,75a

55,25a⁴

<30;

(4)

Sprawdzić, czy naprężenia normalne działające w belce, przedstawionej

na rys. 4.6.1 nie przekraczają wytrzymałości obliczeniowych, jeżeli;

P = 3 kN, q = 2,4 kN/m,! = 10 m, b = 10 cm, h = 30 cm, f* = 100 MPa, f*. = 40 MPa.

b

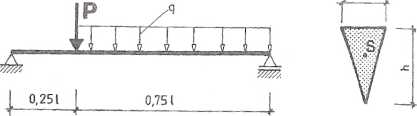
t

Rys. 4.6.1

Rozwiązanie

I -bh³_ 0.1(0,3)³ x 36

36

4.6.1. Obliczenie momentu bezwładności (rys. 4.6.2d) 75-IO^m⁴.

4.6.2. Obliczenie oddziaływań podpór (rys. 4.6.2a)

]PM_a = 0 ; P 2,5+q 7,5(2,5 + 3,75) - V_B10 = 0;

XM_B = 0 ; -p 7,5-q 7,5 ■ 3,75+ V_B10 = 0.

Stąd:

V_A = 9 kN, Vb= 12 kN.

4.6.3. Funkcje sił wewnętrznych Przedział l - z e (0;2,5),

M(z)= V_A z- 9z;

M(0)= 0; M(2,5)= 22,5 kNm;

T(z)= V_A = 9 kN.