skanuj0111 (18)

202 B. Cieślar

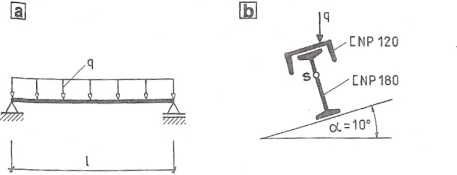
Rys. 5.4.1

Maksymalny moment zginający:

M= i-= 5^1 = 22,5 kNm. o o

Ponieważ wektor momentu zginającego nie leży na żadnej głównej, centralnej osi bezwładności przekroju, więc jest to przypadek zginania ukośnego.

Rozkładając wektor M na składowe wzdłuż osi „x” i „y” mamy:

M_x = Mcosa = 22,5-cos(10°) = 22,16 kNm;    =>    M_x = - M_x;

M_y = Msina = 22,5-sin(10°) = 3,91 kNm;    =>    M_y = + M_y.

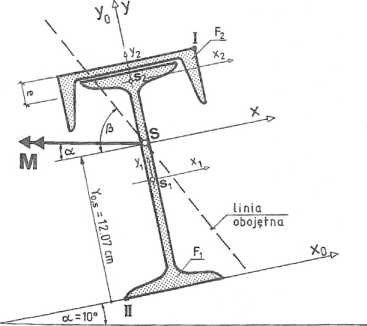
Rys. 5.4.2

V. Zginanie ukośne___ 203

Wzór do obliczania naprężeń normalnych ma w tym przypadku następującą postać:

-M_xy M_yx _ -22,5 ■ 100 y 3,91 • 100x ^G J_x J_y *    2186,3    445,3 ¹

gdzie:

o - naprężenie normalne w [kN/cm²],

x, y - współrzędne punktu (w cm), w którym obliczamy naprężenie. Równanie linii obojętnej:

a = 0;    y = -0,87x.

Z położenia linii obojętnej (rys. 5.4.2) wynika, iż największe naprężenia będą w punktach I i II, których współrzędne są następujące:

X| = 6cm; yi = 6,63cm;

Xn = - 4,1 cm; yu = - 12,07cm.

Sprawdzenie naprężeń:

-22,16 >100 6,63 3,91-100 6 2186,3    445,3

= -12,0-Ą- = -120,OMPa, cm

,-22,16 -100 (-12,07) 3,91 100 (-4,1)

2186,3

445,3

= 15,84

kN

158,4MPa.

Tak więc największe, co do wartości bezwzględnej, naprężenia normalne nie przekraczają wytrzymałości obliczeniowej f_d = 215 MPa.

HH

Do stalowej belki o przekroju dwuteowym (rys. 5.5.1) przyłożono pionowo

obciążenie równomiernie rozłożone q oraz poziomo siłę P. Obliczyć największe naprężenie normalne w belce. Dane: q = 10 kN/m, P = 4 kN, I = 4 m.

Rozwiązanie

Określimy najpierw momenty zginające od obciążenia „q” (rys. 5.5.2a). Z równań równowagi ^M_x = 0 i ^M_x = 0 obliczamy:

RAy = 0,5ql, Rc_y m 0,5ql.

Pozostałe reakcje są równe zeru.