skanuj0161 (2)

169

Powyższe rozważania dotyczyły kształtowania się produkcyjności całkowitej, kratkowej i przeciętnej przy działaniu prawa wydajności nieproporcjonalnej.

W warunkach, gdy działa prawo wydajności proporcjonalnej, produkcyj ność krańcowa kolejnych nakładów czynników zmiennych, jak również produkcyjność przeciętna jest stała w całym przedziale od minimum do maksimum całkowitej produkcji. Czyli produkcyjność przeciętna jest równa produkcyjności krańcowej przy każdym nakładzie czynników wytwórczych (rys. 8.9). Krzywe produktu krańcowego i przeciętnego są w tym wypadku liniami prostymi, równoległymi do osi odciętych. Jak pamiętamy, w warunkach działania prawa wydajności proporcjonalnej krzywa produkcji całkowitej jest linią prostą, wychodzącą z początku układu współrzędnych, co oznacza, że produkt całkowity rośnie proporcjonalnie do wielkości nakładów czynników wytwórczych.

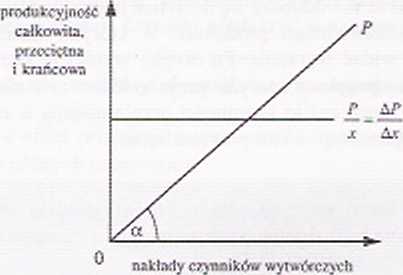
Rys. 8.9. Produkcyjność całkowita, przeciętna i krańcowa w warunkach, działania prawa wydajności proporcjonalnej

Miarą geometryczną produkcyjności krańcowej i przeciętnej

jest tg <j Ct, który wyraża stałą produkcyjność przeciętną, jak i równą jej stałą produkcyjność krańcową.

Na koniec rozważanych wyżej zagadnień należy podkreślić, że niepropor-cjonainość wzrostu produkcji uwidacznia się bardziej wtedy, gdy mamy do czynienia z wytwarzaniem jednego i jednorodnego produktu (np. energii elektrycznej czy cementu). Gdy liczbę angażowanych w procesie produkcji zmiennych czynników wytwórczych ograniczymy do kilku, przy czym jeden z nich będzie odgrywał rolę dominującą, wzajemne oddziaływanie produkcyjności różnych zmiennych czynników radykalnie się zmniejsza. Odpadają wtedy także dodatkowe czynniki (np. zmienność asortymentu, długość serii itp.), które w pizypad-