skanuj0202 (5)

belki (wału) równa się algebraicznej sumie momentów wszystkich sił, działających po jednej stronie rozpatrywanego przekroju...”. Stąd

Mgły	= o,			Mg ix =	o,
MgAy	= 110	N	■ m,	MgAX =	131 N-m,
Mg2y	= 351	N-	m,	Mg2x ~	46 N-m,
Mg 3,	= 252	N-	m,	Mg 3x =	— 39N-m,
MgBy	= 0,			MgBx =	0.

Wyznaczamy wartości momentów zginających wypadkowych

M_gA = jM²gAx+M²gAy = J 131² + 110² * 171 N-m oraz: M_g2 = 354 N • m, M_g3 = 255 N • m, M_gl = M_gB = 0.

Dla obliczenia momentów zastępczych M. wyznaczamy wartość momentu skręcającego z uwzględnieniem współczynnika (tzw. momentu zredukowanego). Z tabl. 1.4 — k_go = 70 MPa, k_so = 40 MPa, stąd

Ko 70

a = —^ = — = 1,75 k„ 40

M'_sl =

Ml, =

a - Af 2

a - M_r

sl

1,75-170,5

150 N • m

1,75-102,3

90 N-m

m;₃ =

2

1,75 • 68,2 2

60 N-m

Następnie

M_zl =M'_Si = 150 N-m

M_z/t = JM²a + M'² = 7l71²+ 150² « 227 N-m M_z2 = VM²2 + M;²! = 7354² + 150² « 384 N-m M_z3 = 7M²3 + M;²3 = 7255² + 60² w 262 N-m

^MzB =    0

Obliczamy średnice czopów wału pod koła i łożyska

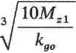
'10-150

70

2,78 cm

oraz: d^ ^ 3,19 cm, d₂ ^ 3,80 cm, d₃ 3,35 cm

Przyjmujemy średnice normalne: di = 30 mm, d_A = 34 mm, d₂ = 40 mm, d₃ = 36 mm i ustalamy kształty wału (rys. 9.8).

Rozwiązanie 2 — metodą półwykreślną Wartości M_s, M', F_x i F_y obliczamy metodą rachunkową.

Przyjmujemy podziałki rysunkowe zapewniające czytelność wykresów. W tym

N

przykładzie przyjęto podziałkę długości: k, = 10, podziałkę sił k_f = 500-oraz

cm

odległość biegunową H = 3cm = 0,03 m.

Obliczamy podziałkę momentów.

^km — ^Kt ■ k_f - H = 10 • 500 • 0,03 = 150

N-m

cm

N

[%] = 1---m = 1

cm

202