img089

ma rozkład x² o ⁴ stopniach swobody (liczba stopni swobody równa się tutaj sumie ilości stopni swobody tablic składowych). Ponieważ

0.05 X?4) - 9.49

więc

X,pról>y ^ 0,05 X(4)

co świadczy o nieistotności różnic pomiędzy próbami.

Dla zbadania zależności pomiędzy partiami obliczamy składnik

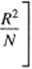
A

II"

rtu

Xprółhi'

L- parto

Pd-P) co odpowiada zagregowaniu czterech tablic z tabeli 6.11. utworzeniu z ich sum brzegowych dwóch tablic pokazanych w tabeli 6.12 i utworzeniu na podobnych jak poprzednio zasadach „sumy” wyrażeń x² dla obu tablic.

Tabela 6.12

Przekształcenie danych z tablicy kontyngencji przedstawionej w tabeli 6.10 dla potrzeb badania zależności pomiędzy partiami (por. także lab. 6.11)

Środek A    Środek B

		*2				b2
Padły	92	91	183	Padły	85	78	163
Przeżyły	7	5	12	Przeżyły	13	20	33
	99	96	195		98	98	196

Dokonując obliczeń otrzymujemy:

(V_ 5i__12^\ /13^ 20:

₂    _ ^V99 ⁺ 96    195^98 * 98 ⁺ 196'

^Xp“^r'^;c    0,8849 0,1151

89