skrypt086

170 Laboratorium {‘odstaw Elektrotechniki 1

Rys.l 1 4. Wykres wskazowy obwodu 2 rys. I 1.3. (rezonans fazowy).

Składowa bierna prądu gałęzi pojemnościowej jest równa składowej biernej prądu gałęzi indukcyjnej. Zbadajmy obecnie rezonans amplitudowy analizowanego dwójnika.

Prąd 1 osiągnie wartość minimalną wtedy, gdy moduł admitancji dwójnika Y dany zależnością

y = Vc²1 if (ii.i5) osiągnie również wartość minimalną.

Pulsację rezonansu amplitudowego tO_ra możemy wyznaczyć z zależności

dco

(11.16)

Tracąc trochę na ogólności rozwiązania, obliczenia przeprowadzić można dla konkretnych wartości liczbowych. Przy danych parametrach C = 0.25 F, L = 1 11, R = 1 £1 otrzymamy

g = -

1 + co

0.25-co (co² -3) co ² +1

(11.17)

_v Vco^fi-6⁴ -h9² + 16

więc. Y — —---^- ,— -

4(CO ² + 1)

Z obliczeń wynika, że jedynym pierwiastkiem równania (11.16) jest wartość pulsacji rezonansu amplitudowego (O_ia=1.975 .

Z warunku rezonansu fazowego B = 0 mamy

co ²-3 = 0 => o_r73-1.732

Wartość pulsacji rezonansu fazowego jest inna niż wartość pulsacji rezonansu amplitudowego.

Na rys. 11.5 przedstawiano graficznie zależności admitancji dwójnika w funkcji pulsacji.

Rys.11.5. Charakterystyki częstotliwościowe admitancji dwójnika z rys.) 1 .'i. o danych C = 0.25 F, L » 1 H, R = 1 O.

11.1.3. Wielkości charakteryzujące obwód rezonansowy a) Dobroć obwodu rezonansowego

_ / wartość składowej biernej pojemnościowej lub indukcyjnej _s (2^— \    —    ■ )cn

wartość składowej czynnej    r

W stanie rezonansu w obwodzie szeregowym RLC dobroć cewki

Ql =

Oi_nL

_ zzo

R

jest równa dobroci kondensatora Q_c =

R(X>₀C

, oznaczamy ją literą

Q i nazywamy dobrocią obwodu szeregowego

gdzie p = Có^L =---

Oi₀C

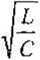
jest impedancją charakterystyczną lub falową

obwodu.

W obwodzie równoległym w stanie rezonansu dobroć obwodu określona jest wzorem