str275

§ 2. PODSTAWOWE DZIAŁANIA ALGEBRAICZNE 275

§ 2. Podstawowe działania algebraiczne

Definicja 1. Sumą dwóch tensorów    i Btego samego typu rzędu M+L

nazywamy tensor Cj,¹*²"'*", którego składowe są sumami tych samych składowych tensorów    i Bff*, co możemy zapisać w następującej formie:

/o 11    f^kik₂...kia _ .kik₂...kM , Dkiki—kM

\*"^l>    WlSJ...*Ł ^_ -^SlS2...SL T-°SlS2...S_Ł *

Własność 1. Dodawanie tensorów jest przemienne

(2.2)    Aⁱs+B^k, = B^k,+A^k.

Własność 2. Dodawanie tensorów podlega prawu łączności

(2.3)    (A^ka+Bt)+C* = A^kMBt+CZ).

Definicja 2. Różnicą dwóch tensorów

_ nkik2..‘kM

^SlSl—SL ^SiSz-^SL.

nazywamy taki tensor    , który czyni zadość równaniu

(2.4)    = <£::*“■

Z definicji 2 wynika, że składowymi różnicy tensorów jest tensor utworzony z różnic składowych o tych samych wskaźnikach tensorów od siebie odejmowanych.

Definicja 3. Pomnożyć tensor przez liczbę (skalar), to znaczy pomnożyć każdą jego składową przez tę liczbę (skalar).

Własność 3. Kombinacja liniowa tensorów tego samego rodzaju i rzędu jest również tensorem tego samego rodzaju i rzędu np.

(2.5)    aA^kr + bB^kr + cC^ks^r = 7’/', gdzie a, b, c są dowolnymi liczbami rzeczywistymi. .

Definicja 4. Tensorem symetrycznym względem jakiejś pary wskaźników (jednocześnie górnych lub jednocześnie dolnych) nazywamy tensor, którego wartości składowe nie zmieniają się przy wzajemnym przestawieniu tych wskaźników np.

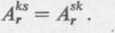
(2.6)

Własność 4. Tensor symetryczny pozostaje symetrycznym po dokonaniu transformacji układu współrzędnych, np. jeżeli

to

= A‘

r.c    s;

Al = AL

gdzie

A'_r^ls] = A

dx"

dx‘

d7^s

Definicja 5. Symetryzacją nazywamy operację, która przypisuje danemu tensorowi

18*