Transport06

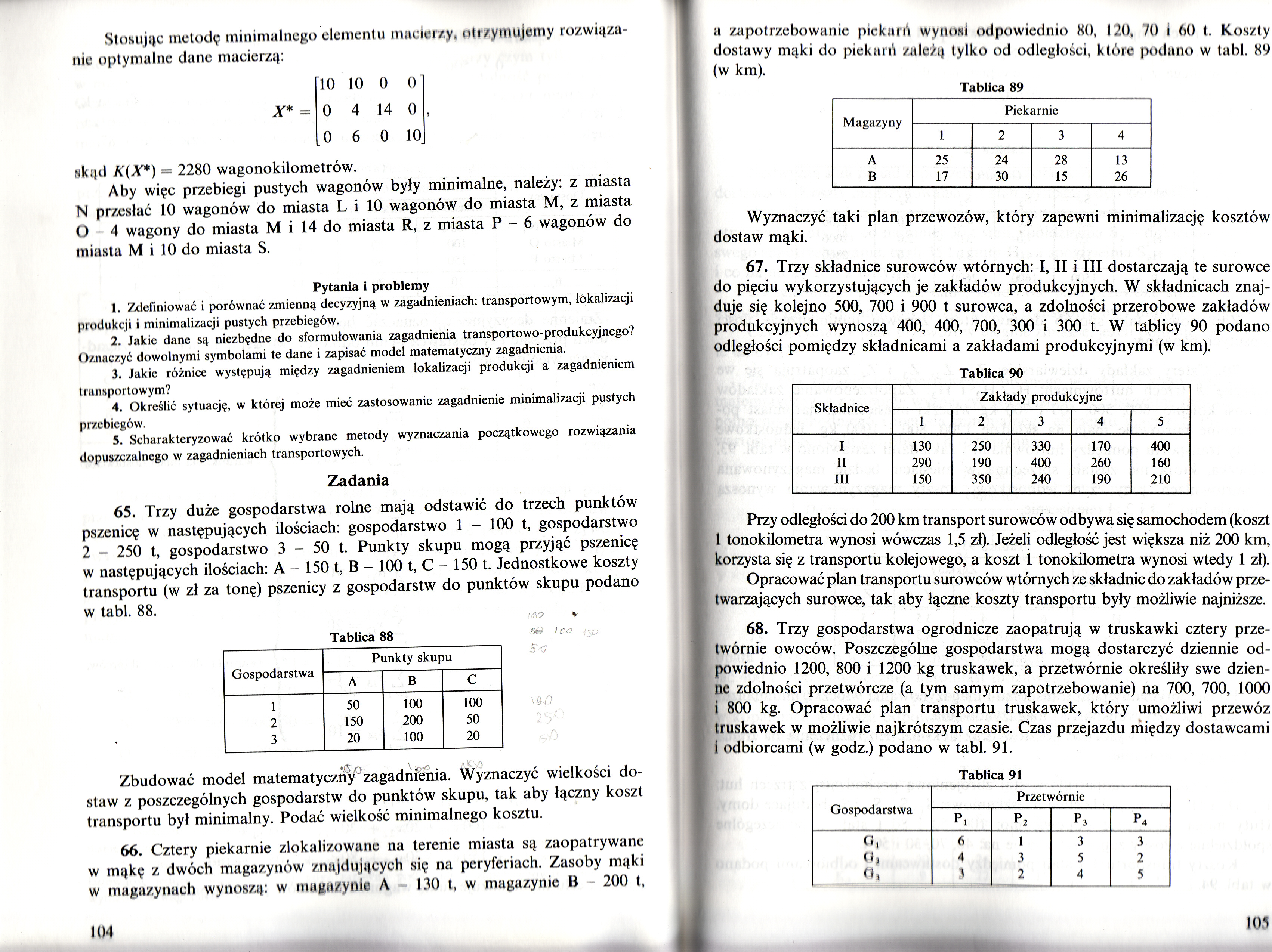
Stosując metodę minimalnego elementu macierzy, otrzymujemy rozwiązanie optymalne dane macierzą:

X* =

10	10	0	0
0	4	14	0
0	6	0	10.

skąd K{X*) = 2280 wagonokilometrów.

Aby więc przebiegi pustych wagonów były minimalne, należy: z miasta N przesłać 10 wagonów do miasta L i 10 wagonów do miasta M, z miasta O 4 wagony do miasta M i 14 do miasta R, z miasta P - 6 wagonów do miasta M i 10 do miasta S.

Pytania i problemy

1.    Zdefiniować i porównać zmienną decyzyjną w zagadnieniach: transportowym, lokalizacji produkcji i minimalizacji pustych przebiegów.

2.    Jakie dane są niezbędne do sformułowania zagadnienia transportowo-produkcyjnego? Oznaczyć dowolnymi symbolami te dane i zapisać model matematyczny zagadnienia.

3.    Jakie różnice występują między zagadnieniem lokalizacji produkcji a zagadnieniem transportowym?

4.    Określić sytuację, w której może mieć zastosowanie zagadnienie minimalizacji pustych przebiegów.

5.    Scharakteryzować krótko wybrane metody wyznaczania początkowego rozwiązania dopuszczalnego w zagadnieniach transportowych.

Zadania

65. Trzy duże gospodarstwa rolne mają odstawić do trzech punktów pszenicę w następujących ilościach: gospodarstwo 1 - 100 t, gospodarstwo 2    250 t, gospodarstwo 3 - 50 t. Punkty skupu mogą przyjąć pszenicę

w następujących ilościach: A - 150 t, B - 100 t, C - 150 t. Jednostkowe koszty transportu (w zl za tonę) pszenicy z gospodarstw do punktów skupu podano w tabl. 88.

\0O V

Tablica 88

Gospodarstwa	Punkty skupu
	A	B	c
1	50	100	100
2	150	200	50
3	20	100	20

\M

I DO jrp

Zbudować model matematyczny⁰zagadnienia. Wyznaczyć wielkości dostaw z poszczególnych gospodarstw do punktów skupu, tak aby łączny koszt transportu był minimalny. Podać wielkość minimalnego kosztu.

66. Cztery piekarnie zlokalizowane na terenie miasta są zaopatrywane w mąkę z dwóch magazynów znajdujących się na peryferiach. Zasoby mąki w magazynach wynoszą: w magazynie A 130 t, w magazynie B 200 t, u zapotrzebowanie piekarń wynosi odpowiednio KO, 120, 70 i 60 t. Koszty dostawy mąki do piekarń zależą tylko od odległości, które podano w tabl. 89 (w km).

Tablica 89

Magazyny	Piekarnie
	1	2	3	4
A	25	24	28	13
B	17	30	15	26

Wyznaczyć taki plan przewozów, który zapewni minimalizację kosztów dostaw mąki.

67. Trzy składnice surowców wtórnych: I, II i III dostarczają te surowce do pięciu wykorzystujących je zakładów produkcyjnych. W składnicach znajduje się kolejno 500, 700 i 900 t surowca, a zdolności przerobowe zakładów produkcyjnych wynoszą 400, 400, 700, 300 i 300 t. W tablicy 90 podano odległości pomiędzy składnicami a zakładami produkcyjnymi (w km).

Tablica 90

Składnice	Zakłady produkcyjne
	1	2	3	4	5
I	130	250	330	170	400
II	290	190	400	260	160
III	150	350	240	190	210

Przy odległości do 200 km transport surowców odbywa się samochodem (koszt I tonokilometra wynosi wówczas 1,5 zł). Jeżeli odległość jest większa niż 200 km, korzysta się z transportu kolejowego, a koszt 1 tonokilometra wynosi wtedy 1 zł).

Opracować plan transportu surowców wtórnych ze składnic do zakładów przetwarzających surowce, tak aby łączne koszty transportu były możliwie najniższe.

68. Trzy gospodarstwa ogrodnicze zaopatrują w truskawki cztery przetwórnie owoców. Poszczególne gospodarstwa mogą dostarczyć dziennie odpowiednio 1200, 800 i 1200 kg truskawek, a przetwórnie określiły swe dzienne zdolności przetwórcze (a tym samym zapotrzebowanie) na 700, 700, 1000 i 800 kg. Opracować plan transportu truskawek, który umożliwi przewóz truskawek w możliwie najkrótszym czasie. Czas przejazdu między dostawcami I odbiorcami (w godz.) podano w tabl. 91.

Tablica 91

Gospodarstwa	Przetwórnie
	P,	P2	P3	P4
Ol	6	1	3	3
Ol	4	3	5	2
o,	J	2	4	5

105