zad13

1.12) Fabryki A_u A₂ i A₃ produkują żarówki w liczbie: n_x = 50000, «₂ ⁼ 80000 i «₃ = 20000. Wiadomo, że fabryki te produkują przeciętnie 0,3; 0,2 i 0,5% wadliwych żarówek. Określić, z której fabryki najprawdopodobniej pochodzi zakupiona wadliwa żarówka. Przedstawić sposób otrzymania odpowiedzi z użyciem drzewa doświadczenia.

Rozwiązanie: Oznaczając przez A_v A₂, A₃ zdarzenia polegające na tym, że żarówka pochodzi odpowiednio z fabryki A_t, A_z, A₃ oraz przez B zdarzenie polegające na tym, że zakupiona żarówka nie nadaje się do użytku, przy uwzględnieniu danych zadania oblicza się prawdopodobieństwa wyprodukowania żarówek w każdej z fabryk (prawdopodobieństwo a priori zdarzeń A_lt Ą, A₃):

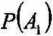
50000    _ 5

«i +«₂ ⁺ⁿ3 ~ 50000+80000 + 20000 ” 15 ’

p(ą)

p(ą)

«2	80000	8
^U\ ^+rł2 +^W3	” 50000+80000 + 20000	” 15 ’
«3	20000	2
«, +n2 +n3	” 50000+80000 + 20000	15

Następnie oblicza się prawdopodobieństwa warunkowe:

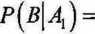
0,3-10^-50000

50000

15

5000’

p{b K)=

0,2 -10^² -80000 _ 16 80000 8000’

0,5-10"²-20000    10

20000 ” 2000

Na podstawie wzoru Bayesa po wykonaniu obliczeń otrzymuje się prawdopodobieństwa a posteriori przyczyn:

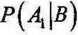
P(ffn4)

P(B)

_^)-^)

p(ą)-p(b\ą)+p(ą)-p(b\a₂)+p(a₃)-p(b\a₃)

5_    15

15 5000_₌ i1

_5_ _ii_    ²    10    41’

15 5000 ⁺ 15 8000 ⁺ 15 2000

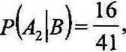
Zakupiona wadliwa żarówka pochodzi najprawdopodobniej z fabryki A₂.

Diagram (drzewo) doświadczenia przedstawia rys. 2.2. Drzewo ma począ tek (korzeń) w punkcie K. Węzły, w których umieszczono wyniki kolejnycl etapów doświadczenia, są łączone odcinkami (krawędziami). Przy każdej kra wędzi jest podane prawdopodobieństwo otrzymania wyniku danego etapu do świadczenia. Gałęzią drzewa jest ciąg krawędzi łączący początek drzewa z do wolnym z węzłów końcowych. Każdej gałęzi odpowiada prawdopodobieństw

doświadczenia wieloetapowego, które jest równe iloczynowi prawdopodobieństw poszczególnych krawędzi tworzących gałąź.

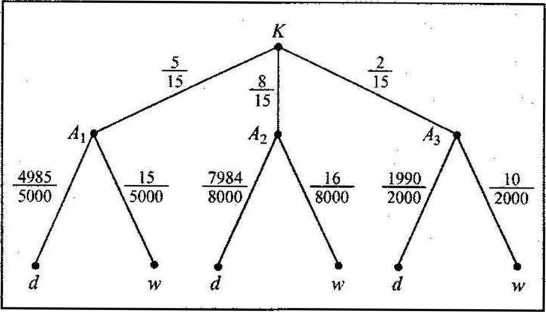
Rys. 2.2. Rozwiązanie z użyciem drzewa doświadczenia (d - żarówka dobra, w - żarówka wadliwa)

Prawdopodobieństwa zakupienia żarówki wadliwej pochodzącej z każdej z fabryk A_t,A₂, A₃ wynoszą kolejno:

P(BnĄ) = ±

p(_B)=±.J^ ₊ ±

5	15	15
15	5000	” 15000’
8	16	16
15	8000	o o o m n—1 1
2	10	10
15	2000	”15000’
15	8	16 2

10

• +---

15 5000 15 8000 15 2000

41

15000 '

Sumując iloczyny prawdopodobieństw w gałęziach zakończonych węzła mi w, otrzymuje się prawdopodobieństwo całkowite P(b). Największe prawdo podobieństwo dla gałęzi (a₂, w) wskazuje, że zakupiona wadliwa żarówka po chodzi najprawdopodobniej z wytwórni A₂.