Untitled Scanned 17

- 34 -

tablicy zapełnia Bię wartościami funkcji, odpowiadającymi poszczególnym stanom argumentów. Dla ułatwienia wypełniania tablic na podstawie zapisów symbolicznych funkcji, w polach wewnątrz tablic na rys.2.1 wypisano numery stanów argumentów odpowiadających tym polom.

^01X		JL	1		b)	\»2*3 *1X00			01	11	10
	0	0	1				0	o	1	— 3	?i
	1	2	3				1	4	5	7	ci
C)				d)
V3 *1^	<4 ' 09	01	11	10	*1*2\	1*5 000	001	on	010	110	m	101	W
00	Q	1	3	7,	00	9	1	3	7.	6	7	?	4
01	4	5	7	ę	01	8	9	11	1Q	14	15	13	12
11	12	i?	!5	14	11	24	25	27	?§	?o	3*	3?	??
10	6	9	11	-12	10	-lfi	-12	Jfi	JŁ	22	23		~2&i

Rys.2.1. Tablice Karnaugha dla funkcji dwu-, trój-, cztero- i pięcioargumentowych

Stany argumentów wypisane są na obrzeżach tablic zgodni, z kolejnymi znakami kodu Graya. Dzięki temu składniki Jedności lub czynniki zera, odpowiadające sąsiednim polom (sąsiednimi są np. na rys.2.1 pola 014, 0i2, 0 i 1, U 6 itć.) mogą być sklejane, gdyż różnią się jednym tylko znakiem negacji. Iloczyny lub sumy odpowiadające "sąsiednim" parom pól także mogą być sklejane. Podobnie mogą być sklejane iloczyny lub sumy odpowiadające "sąsiednim" czwórkom pćl itd. "Sąsiednie" pola, pary pól, czwórki pól rozpoznawać można po tym, że odpowiadające im stany argumentów różnią się wartością jednej tylko pozycji.

Minimalizacja funkcji zapisanej w tablicy Karnaugha polega na:

-    wyszukaniu możliwie dużych, nadających się do sklejenia grup jedynek albo zer,

-    wyborze zestawu tych grup, obejmującego wszystkie jedynki albo wszystkie zera,

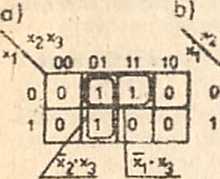
t		ii 1
1	0 |	1

BL^ł

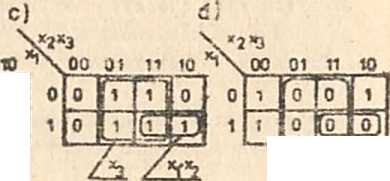
>"^*2

Rye.2.2. Przykłady sklejania w tablicach funkcji trójargumentowych

o)    b)    c)

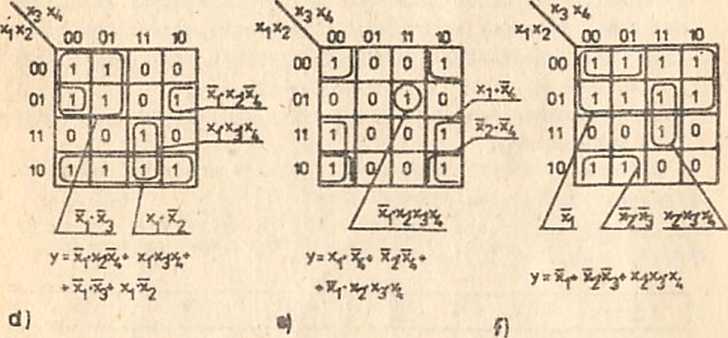
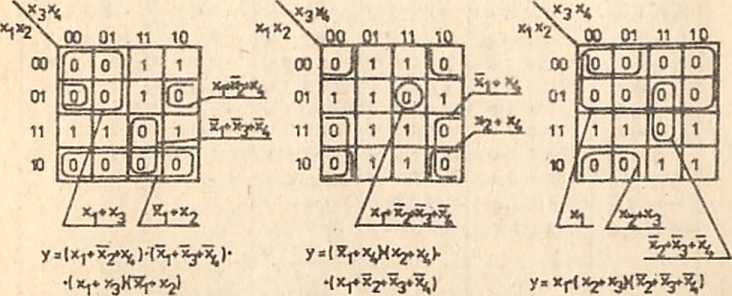
Rys.2.3. Przykłady sklejania w tablicach funkcji czteroargu-

nentowych