Untitled Scanned 13

- 26

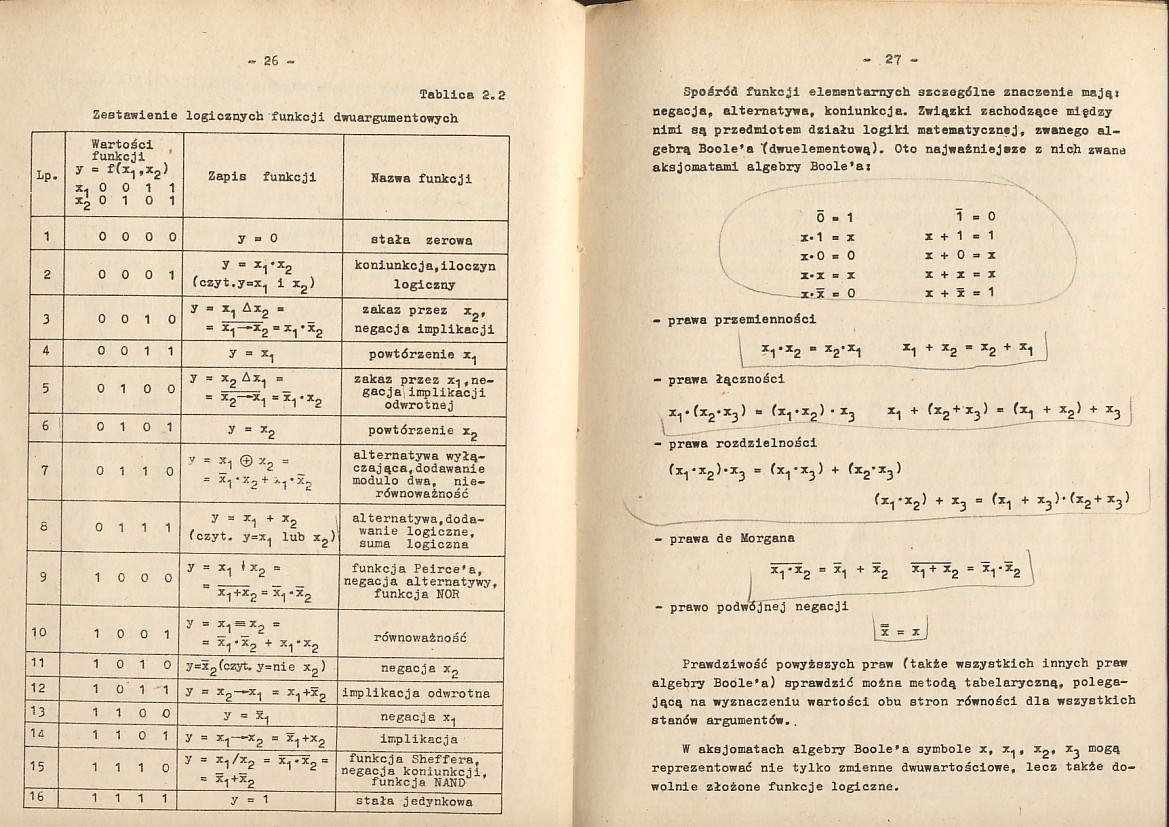
Tablica 2.2

Zestawienie logicznych funkcji dwuargumentowych

Lp.	Wartości funkcji y = fCxvx2 x. 0 0 1 x2 0 1 0			t ) 1 1	Zapis funkcji	Nazwa funkcji
1	0	0	0	0	y o 0	stała zerowa
2	0	0	0	1	y - Vx2 fczyt.y=x1 i xg)	koniunkcja,iloczyn logiczny
3	0	0	1	0	y » x1 Ax2 » “ x1^x2 = x1-x2	zakaz przez x2, negacja implikacji
4	0	0	1	1	y = x1	powtórzenie x^
5	0	1	0	0	y = x2 Ax1 o = X2~“X-J » X1 • Xg	zakaz przez x-j,negacja implikacji odwrotnej
6 '	0	1	0	1	y * x2	powtórzenie x2
7	0	1	1	0	y = x1 0 *2 = = x.j • *2 + *1*^2	alternatywa wyłączaj ąca,dodawanie modulo dwa, nie-równowainość
6	0	1	1	1	y a x1 + x2 (czyt. y=x1 lub x2)	alternatywa,dodawanie logiczne, suma logiczna
9	1	0	0	0	y = x1 lz2 a ^*^2 ^= ^*| * ^2	funkcja Peirce»a, negacja alternatywy, funkcja NOR
10	1	0	0	1	y = = *2 = = X1• Xg + X1-X2	równoważność
11	1	0	1	0	yex2Cczyt. y=nie xg)	negacja x2
12	1	0‘	1	1	y = ^X2“^^X1 = ^xi^+x2	implikacja odwrotna
13	1	1	0	0	y - s.	negacja x1
ic	1	1	0	1	y = x^—»x2 = x^+x2	implikacja
15	1	1	1	0	y ^= x1/x2 — x^•x2^== x1+x2	funkcja Sheffera, negacja koniunkcji, funkcja NAND
16	1	1	1	1	y o 1	stała jedynkowa

Spośród funkcji elementarnych szczególne znaczenie mająi negacja, alternatywa, koniunkcja. Związki zachodzące między nimi są przedmiotem działu logiki matematycznej, zwanego algebrą Boole*a Tdwuelementową). Oto najważniejsze z nich zwane aksjomatami algebry Boole*a*

0 - 1 X»1 = X x» 0 b 0 X-X B X x*x « 0

1=0 x + 1 - 1 x + 0 = x

X + X = X X + X = 1

-    prawa przemienności

XyX₂ - X₂-X₁    x^ + X₂ - X₂ + X₁

-    prawa łączności

L¹'

(x₂*x^) « (x₁»x₂)*x^    X-, + fx₂+ x₃) - fx₁ + x₂) + x₃

-    prawa rozdzielności

fx₁*x₂)«x₃ B (x₁'Xj)    +    (x₂*x₃)

fx₁*x₂) + x₃ B fx₁ + x₃)’fx₂+x₃)

- prawa de Morgana

m5 Jn

* ^X1 ⁺ x2 ^x,\ ⁺ x2 ^s X1‘^X2

- prawo podwójnej negacji

|S-xJ

Prawdziwość powyższych praw (także wszystkich innych praw algebry Boole*a) sprawdzić można metodą tabelaryczną, polegającą na wyznaczeniu wartości obu stron równości dla wszystkich stanów argumentów..

W aksjomatach algebry Boole*a symbole x, x₁, x₂, x₃ mogą reprezentować nie tylko zmienne dwuwartościowe, lecz także dowolnie złożone funkcje logiczne.