zg 2

Ad d) Zasada de Saint Venanta weryfikowana jest na belce wysięgnikowej o skokowo zmiennym przekroju (sztywność EJ - stała odcinkami, zmienna skokowo). Tensometry oporowe umieszczone są na belce zarówno w bezpośredniej bliskości, jak i w dużym oddaleniu od stref, których dotyczy zasada de Saint Venanta. Stosowalność tej zasady wykazuje się porównując wyniki pomiarów z obliczeniami wg podstaw WM.

Ad e) Korzystając z zależności definiującej krzywiznę pręta w stanie czystego zginania

można obliczyć teoretyczne ugięcia maksymalne (strzałkę ugięcia) w obszarze czystego zginania:

f — w —

./    max

Ml²

8EJ

(e.2)

Notując wskazania czujników przemieszczeń w odpowiednim punkcie w funkcji obciążenia (np. 5-7 pomiarów dających wykres f(Mg)) należy obliczyć wartość modułu Younga materiału.

W tym punkcie weryfikujemy także kształt linii ugięcia belki dla stałego momentu

zginającego, Mg = const. (wykres w(x)).

Ad f) Dla odpowiedniej belki, wskazanej przez prowadzącego, wykonać pomiary ugięcia belki w pewnym punkcie i porównać wyniki analityczne [1] z wynikami doświadczenia.

Belka (duralowy kątownik nierównoramienny) na dwóch podporach obciążona jest dowolną konfigui icją sił wprowadzanych w półki kątownika (uwaga dla bardziej zaawansowanych: wprowadzane siły przechodzą przez SSP, czyli środek ścinania. Nie zachodzi zatem skręcanie przekroju wywołane mimośrodem).

Na półkach kątownika naklejone są tensometry, mierzące odkształcenia wzdłuż osi pręta w jednym przekroju. Można zatem wyznaczyć rozkład naprężeń cr_x w tym

przekroju. Rozkład naprężeń wg elementarnej teorii ma rozkład płaszczyznowy ([1]). Wyniki pomiarów porównujemy z wynikami analitycznymi wg wzorów (6.4 i 6.3, [1]):

/

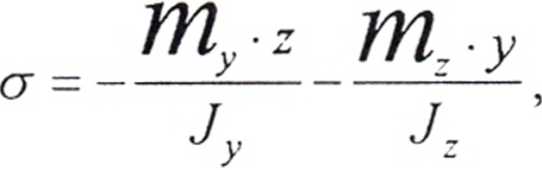
(gl)

gdzie:

✓

v

/

= X

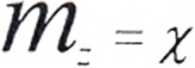
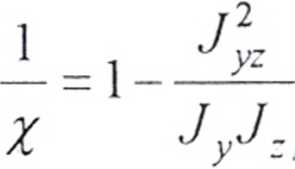
M. - M _v ■

v

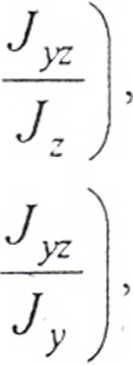
Alternatywnie można skorzystać z innego podejścia analitycznego. Należy wyznaczyć położenie osi głównych analizowanego kątownika i rozłożyć działający moment zginający na wartości składowe działające w płaszczyznach osi głównych. Tak rozłożone wartości składowe podlegają wzorom dla zwykłego zginania poprzecznego. Zginane poprzeczne zachodzące w płaszczyznach osi głównych przekroju podlega

2