66458

Równanie de Saint-Venanta dla szerokości kanału prostokątnego:

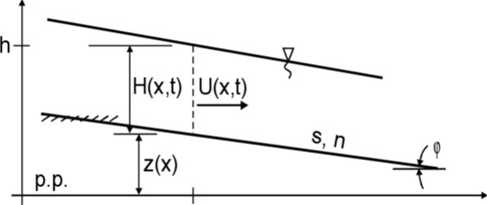
zał.:przepływ w kanale jest jednowymiarowy, przepływ jest wolnozmienny, spadek dna jest mały (sin <p= <p), obowiązuje prawo hydrostatycznej zmiany ciśnienia wzdłuż głębokości, rozkład prędkości w przekroju poprzecznym jest jednostajny, opory ruchu liczy się jak przy przepływie ustalonymStosowane zasady zachowania: masy, pędu: układ równań de Saint-Venanta dla szerokiego kanału prostokątnego: 1) równanie ciągłości: óH/ót + 5/5x(UH)=0; równanie dynamiczne: 5U/6t+U*6U/5x+g5H/5x+g(S-s)=0; RYS; U-prędkość średnia w przekroju,/-/ -głębokość,g - pizyspieszenie grawitacyjne, s - spadek dna, S=n²U|U|/R^w-spadek lini energii

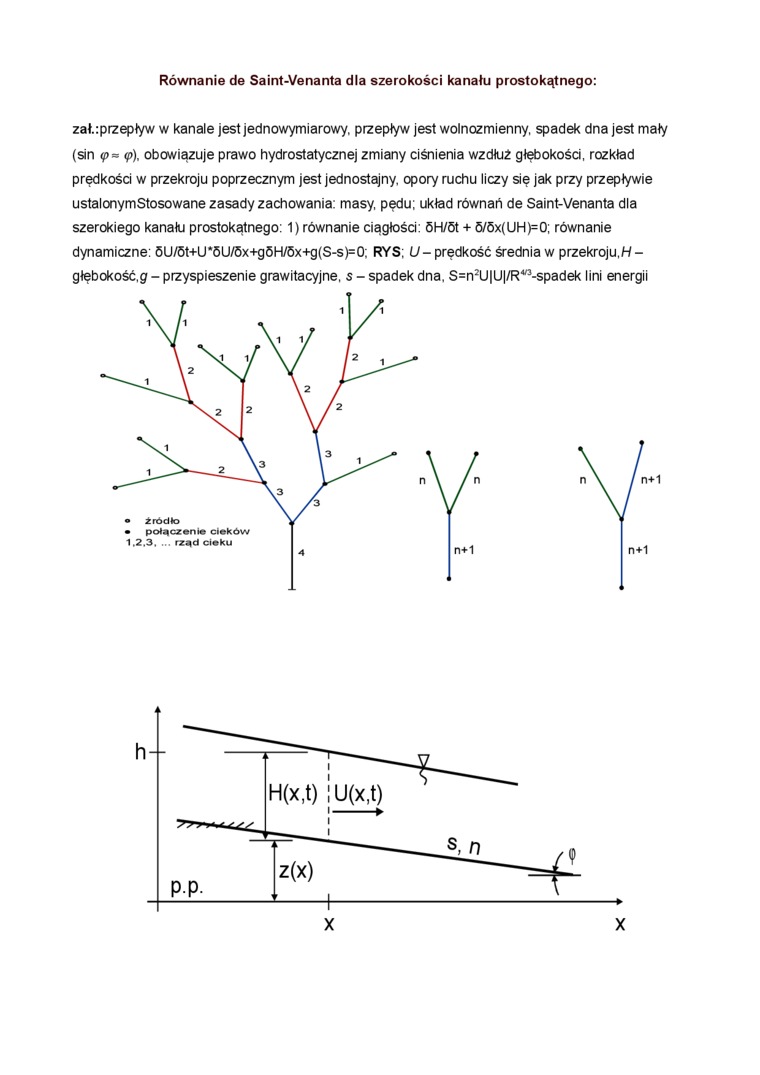
X

X