Image10 (43)

24 Rozwiązania zadań ze zbioru "MENDLA"

n« 100 J-

mol

J~

n = 100 moli

Odp.: W przemianie bierze udział 100 moli gazu doskonałego.

Dane:

p = c-V,

c - stała

Zadanie 552    str.109

Szukane:

P ( T ) = ?

V(T)=?

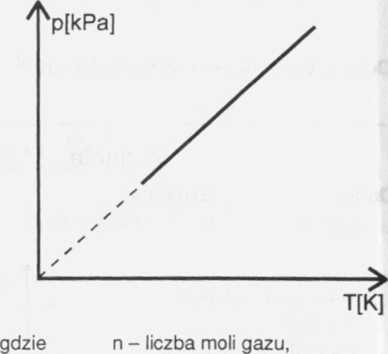
W danej przemianie ciśnienie gazu p jest wprost proporcjonalne do temperatury bezwzględnej T gazu, więc p = c V, gdzie c jest współczynnikiem proporcjonalności.

Z równania stanu gazu doskonałego otrzymamy:

p-V T ="

R /T,

R - uniwersalna stała gazowa.

P

V =

V = n • n - R

/: p

Otrzymane V podstawiamy do związku podanego w zadaniu: p = c V

stąd

n-R-T ,

T" ^Ap

p- = c • n • R • T p = Vc • n • R • VT

Wielkości c, n, R są stałymi, więc pierwiastek z iloczynu tych stałych możemy zastąpić nową stałą A = Vc n R.

Ostatecznie otrzymamy:

p = A • VT - ciśnienie jest proporcjonalne do pierwiastka z temperatury bezwzględnej.

Podobnie wyznaczamy V(T) korzystając z równania Clapeyrona:

p-V T ⁼ⁿ

R,

lecz

p =c • V

stąd ^C'Y— = n- R /T

T

_c . V² = n ■ R • T /: c V² =    ^ . T

-V¥

VT

Wielkości n, R, c, są stałymi

i, więc    i

jest także stałą.

Oznaczamy ją literą B, czyli Po podstawieniu mamy:

V = B • VT - objętość jest również wprost proporcjonalna do pierwiastka drugiego stopnia z temperatury bezwzględnej.

Zadanie 553 str.110

Dane:    Szukane:

p = 0,5 • 10⁵Pa    T = ?

V = 150drr? = 0,150m³ N = 1,8 • 10²⁴

k = 1,38 • 10“ ²³ 7 - stała Boltzmana k

Z równania gazu doskonałego otrzymamy: = N • k AT

p • V = N • k • T /: (N • k)

N-k

0,5 • 10⁵ Pa - 0,15 nr?

T =

T =

1,8-10²⁴ -1,38-10^-23p

A

7500-^ • m³ rrr

_Pa-JL

nf

N ■ m = J