Image18

34

6.4. Wyznaczyć stałą w równaniu Maxwella-Boltzmanna dla cząstek:

a)    o 1 stopniu swobody translacji (poruszających się w jednym wymiarze),

b) o 2 stopniach swobody translacji (poruszających się po powierzchni),

c) o 3 stopniach swobody translacji (poruszających się w przestrzeni).

6.5. Wychodząc z równania Maxwella-Boltzmanna na rozkład pędu w układzie o 1 stopniu swobody znaleźć wzory:

a)    na rozkład prędkości,

b)    na rozkład energii kinetycznej.

6.6. Wychodząc z równania Maxwella-Boltz

II

anna na rozkład składowych

pędu w układzie o 2 stopniach swobody, znaleźć wzory:

a)    na rozkład składowych prędkości,

b)    na rozkład modułu prędkości,

c)    na rozkład energii kinetycznej.

6.7. Wychodząc z równania Maxwella-Boltzmanna na rozkład składowych pędu w układzie o 3 stopniach swobody, znaleźć wzory:

a)    na rozkład składowych prędkości,

b)    na rozkład modułu prędkości,

c)    na rozkład energii kinetycznej.

6.8.    Wyprowadzić wzór na zależność ciśnienia powietrza od wysokości (wzór barometryczny). Traktować powietrze jak gaz doskonały i założyć, że zależność temperatury od wysokości można zaniedbać.

6.9.    Znaleźć względny rozkład koncentracji cząstek koloidalnych w wirówce, po osiągnięciu stanu równowagi. Cząstki koloidu w wirówce traktować podobnie jak cząstki gazu doskonałego.

6.10.    Mamy układ oscylatorów harmonicznych liniowych w stanie równowagi termicznej. Znaleźć gęstość prawdopodobieństwa, że dany oscylator znajduje się w stanie odpowiadającym wychyleniu z położenia równowagi do wielkości z przedziału (x, x -f dx).

co = iw_x 4- jco_y + Kw_z.

a.    Znaleźć rozkład Maxwella-Boltzmanna na liczbę cząstek o module prędkości kątowej rotacji w przedziale (co, co + dco).

b.    Znaleźć rozkład Maxwella-Boltzmanna na liczbę cząstek o energii rotacji w przedziale (E_r, E_r -ł- dE_r).

6.11.    Rozpatrzmy rozkład rotatorów sztywnych (np. w przybliżeniu układ obracających się drobin) o momencie bezwładności I i prędkości kątowej

6.12.    Korzystając z prawa Maxwella rozkładu prędkości cząsteczek gazu, wyprowadzić wzory na prędkość najbardziej prawdopodobną oraz na prędkość średnią.

6.13.    Obliczyć v, v^z i E w układzie:

a)    o 1 stopniu swobody,

b)    o 2 stopniach swobody,

c)    o 3 stopniach swobody.

6.14. Rozrzedzony gaz znajduje się w naczyniu pod ciśnieniem p. Znaleźć prędkość wypływu gazu w próżnię przez niewielki otwór o średnicy S_a, przy założeniu maxwellowskiego rozkładu prędkości cząsteczek gazu.

6.15. Obliczyć v_x dla gazu doskonałego:

a)    dla wszystkich cząstek,

b)    dla cząstek poruszających się w kierunku —x.

6.16. Załóżmy, że energię drobiny można przedstawić w postaci H = E₀ -f E (q/), gdzie E_a jest funkcją pędów i pozostałych współrzędnych uogólnionych oraz załóżmy, że E(q/) -> oo dla q_t -* ± oo. Udowodnić następujące ogólne sformułowanie zasady ekwipartycji energii:

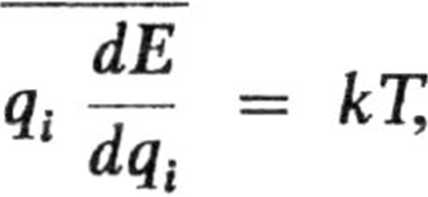
gdzie k jest stałą Boltzmanna. Wykazać, że przy analogicznych założeniach słuszne będzie również twierdzenie:

Pi

dE

dpi

= kT.

6.17. Opierając się na ogólnym sformułowaniu zasady ekwipartycji energii:

a)    wykazać, że na każdy człon w wyrażeniu na energię typu (aq²/2) czy (bp²/2), gdzie a i b - stałe, przypada energia (kT/2),

b)    wyliczyć v² w układach o 1, 2 i 3 stopniach swobody,

c)    wyliczyć średnią wysokość, na jakiej znajdują się cząsteczki powietrza w polu siły ciężkości (założyć, że temperatura nie zależy od wysokości).