Image86 (7)

170
170
(Ijzm k T)1/2
Maxwella-Boltzmanna dla pędu w 1 stopniu swobody, gdzie 1/C Stąd w naszym przypadku
dri =
n
f
2 _
fx2
2kT
2n kT
dx,
tak że gęstość prawdopodobieństwa p(x) wynosi
p(x)
1 dri
fxz 2kT
n dx
2n kT
Zatem średnio najwięcej oscylatorów znajduje się w położeniu równowagi, przy czym liczba ich maleje szybko z kwadratem wychylenia.
6.11
1
a. Energia rotacji wynosi ^ Ico2. Stąd rozkład Maxwella-Boltzmanna przyj
Z#
uje postać
dri
I
2 _
leo1
n I -r—r-=r ) e 2kT d(i)^ dcov dw 2n kT 1 x y
lub przechodząc do współrzędnych sferycznych i wycałkowując po wszystkich możliwych kątach
dri'
Ann
1
2n kT
^ 2 co e
Ico2
2kT dw
b. Podstawiając związek - Iw2 = Er, otrzymujemy
Z#
dn
n
-1 _3 i -h
2nn 1 (kT) 1 E? e ** dE,
6.12. Funkcja rozkładu prędkości cząstek (funkqa rozkładu Maxwella)
4n
m
3
,2
2n kT
2
v e
MO*
21T
przyjmuje wartość zerową dla v = 0 oraz v = co i gdzieś między tymi wartościami osiąga wartość maksymalną. Prędkość najbardziej prawdopodobną vB, odpowiadającą położeniu maksimum tej funkcji, znajdujemy z warunku:
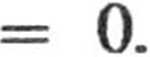
dp(v)
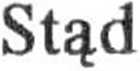



Znając funkcję rozkładu Maxwella ] prędkość cząstek gazu
ożemy napisać wzór określający średnią
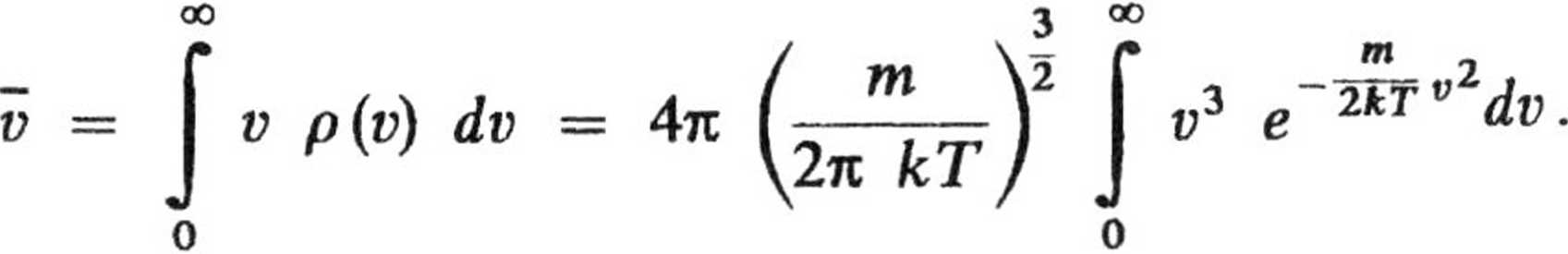
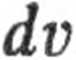
Całkując przez części lub korzystając ze wzoru podanego w rozwiązaniu zad.6.3 mamy
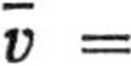

6.13. Przy rozwiązywaniu tych zadań zakładamy, że energia translacji wchodzi addytywnie w energię cząstki.
a. Rozważmy ruch translacyjny z jednym stopniem swobody, np. wzdłuż osi x. Mamy wówczas

oraz
v

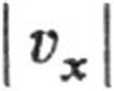
Wyszukiwarka
Podobne podstrony:
16912 Image86 (7) 170 170 (Ijzm k T)1/2 Maxwella-Boltzmanna dla pędu w 1 stopniu swobody, gdzie 1/C
16912 Image86 (7) 170 170 (Ijzm k T)1/2 Maxwella-Boltzmanna dla pędu w 1 stopniu swobody, gdzie 1/C
Image86 (7) 170 170 (Ijzm k T)1/2 Maxwella-Boltzmanna dla pędu w 1 stopniu swobody, gdzie 1/C Stąd w
Image86 170 170 (2nm kT)l/2 Maxwella-Boltzmanna dla pędu w 1 stopniu swobody, gdzie 1/C Stąd w naszy
Image18 34 6.4. Wyznaczyć stałą w równaniu Maxwella-Boltzmanna dla cząstek: a) o 1
134 złomie istotności ot oraz dla ilości stopni swobody k = n - 2. Jeżeli r>r0^n 2 to możemy powi
DSCF2152 134 złomie istotności cx oraz dla ilości stopni swobody k = n - 2. Jeżeli r>r<x,n-2 t
53635 SS854634 9 Przedstawione rozważania można uogólnić dla układów o n — stopniach swobody, dokonu
img110?kłażany z szynką parmeńska 170 DANIA GŁÓWNE MIĘSA 170 DANIA GŁÓWNE MIĘSA Dla 4 osób Czas przy
więcej podobnych podstron