DSCF2152

134

złomie istotności cx oraz dla ilości stopni swobody k = n - 2. Jeżeli ^r>r<x,n-2 ^to możemy powiedzieć, że istnieje 1 - a. prawdopodobieństwo korelacji między zmiennymi.

Tablica 6.5

Współczynnik korelacji r [6.5]

I Stop-I nie swobody	Prawdopodobieństwo wartości bezwzględnej większej lub równej r					Stop nie swoi	Prawdopodobieństwo wartości bezwzględnej większej lub równej r
	0,1	10,05	0,02	0,01	0,001	body	0,1	0,05	0,02	0,01	0,001
1	0,988	10,997	1,0	1,0	1,0	12	0,458	0,532	0,612	0,661	0,780
2	0,900	0,950	0,980	0,990	1.0	14	0,426	0,497	0,574	0,623	0,742
3	0,805	0,878	0,934	0,959	0,991	16	0,400	0,468	0,542	0,590	0,708
4	0,729	0,811	0,882	0,917	0,974	18	0,378	0,444	0,516	0,561	0,679
5	0,669	0,754	0,833	0,874	0,951	20	0,360	0,423	0,492	0,537	0,652
6	0,622	0,707	0,789	0,834	0,925	25	0,323	0,381	0,445	0,487	0,597
7	0,582	0,666	0,750	0,780	0,898	30	0,296	0,349	0,409	0,449	0,554
8	0,549	0,632	0,716	0,765	0,872	35	0,275	0,325	0,381	0,418	0,519
9	0,521	0,602	0,685	0,735	0,847	40	0,257	0,304	0,358	0,393	0,490
10	0,497	0,576	0,658	0,708	0,823	45	0,243	0,288	0,338	0,372	0,465
						50	0,231	0,273	0,322	0,354	0,443

6.3.2. Ustalanie zależności między zmiennymi metodą analityczno-wykreślną

W obróbce ’ skrawaniem większość zależności funkcyjnych wyznacza^ się doświadczalnie. Funkcje te występują zazwyczaj w postaci potęgowej. Przykładem może być funkcja określająca zależność F_y = f(g,p), która ma najczęściej postać»

C -g

(6.26)

W celu wyznaczenia wartości stałej C oraz wykładników potęgowych e ,

z    z

u_B postępujemy wówczas w następujący sposób:

dla p = const zależność (6.26) możemy zapisać;

^Vfc-_v=C₁-g^0Z    (6.27)

oraz dla g = const

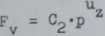
(6.20)

Po zlogarytmowaniu, równania (6.27)' i (6.28) będą miały postacie:

oraz

log P_v = log C₂ + u₂ log p    (6.30)

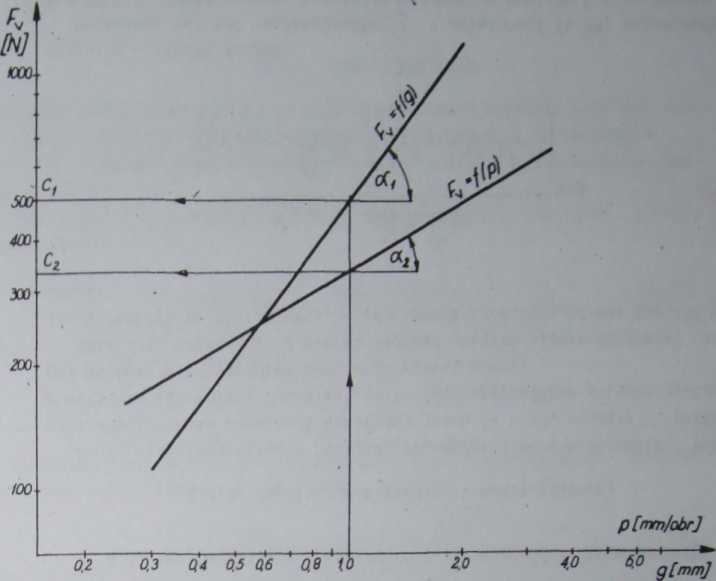
Rys. 6.4. Typowy przebieg zależności F_y = f(g) i F_y = f(p) w układzie logarytmicznym

Zależności (6.29) i (6.30)' przedstawiają równania linii prostych, typu y = mx + b w układzie logarytmicznym. Nanosząo punkty pomiarowe lub średnie z pomiarów zależności F_y = f(g) i F_y = f(p) na układ logarytmiczny, przeprowadzamy proste regresji, na jdŁstawie których możemy określić interesujące nas wartości e_z i u_£ (nie należy uwzględniać punktów obciążonych błędem grubym przy wykreślaniu linii prostej).

Bezpośrednio z wykresów (rys. 6.4) za pomocą kątomierza możemy odczytać wartości kątów i cx₂ lub wyliczyć je z punktów leżących na prostych, których tangensy kątów i oig odpowiadają wartościom współczynników regresji e_z i u₂ (tg = e_z, tg = u_g). Wartości stałych C., i Cp możemy również odczytać z wykresów (dla g = 1 wartość rzędnej odpowiada wartości C^, a dla p = 1 wartości Cg).

Nieznaną wartość stałej C_ w zależności (6.17) możemy wyznaczyć z przekształcenia tej zależności do postaci: