Image22 (26)

42

1.9. Układ współrzędnych wybieramy tak, aby oś x była równoległa, zaś oś y prostopadła do brzegów rzeki. Początek układu przyjmujemy w punkcie startu

łódki.

a. Z lysunku mamy

stąd

v

=

. n y

v_a sm —,

v — ivr + vz sin

ny

L ’

b.

v

dx

dt

dx dy

_____ •

dy dt

= v

dx

¹ d

v, sin

ny

~L

Wobec tego

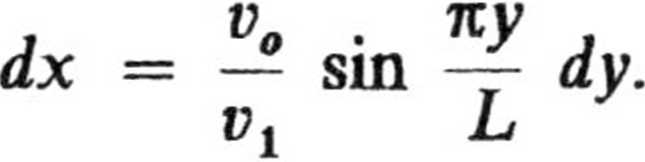
Całkując to równanie, przy warunkach początkowych

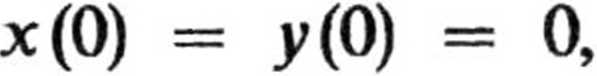
otrzymujemy równanie toru łódki

2 v₀ L

nv_t

ny 2L*

1.10. Przyjmujemy układ współrzędnych jak na rys.9. Wówczas w pierwszej połowie drogi wektor prędkości łodzi będzie miał następujące składowe:

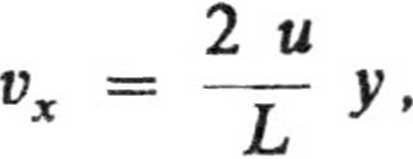
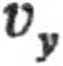
ale

v

dx

dt

= v

dx

dy’

stąd

V

dx

dy

2 u

~L

y

Całkując otrzymane równanie różniczkowe metodą rozdzielenia zmiennych , przy warunkach początkowych t = 0, x = 0, y = 0, dostajemy

1

2^y

v L 2 u

Stąd równanie toru łodzi w pierwszej połowie drogi przybiera postać

Podstawiając do tego równania y = ^ otrzymamy odległość x₀₁, na jaką prąd zniesie łódź

u L

01

Obieramy teraz nowy układ współrzędnych (X' 0' Y') z początkiem w tym punkcie, gdzie znajduje się łódź po przepłynięciu pierwszej połowy drogi (rys.9). Wektor prędkości łodzi ma teraz składowe

2 u

~L

v_x = u

V.

Postępując podobnie jak w przypadku poprzednim mamy

dx!

dy’

U

2 u

L v

V

i