Image23 (27)

50 Rozwiązania zadań ze zbioru "MENDLA"

Stąd H1 = 5_P?

T1    l2

pi • T2 = 3 • p2 • Ti

pi - ciśnienie na głębokości h, więc: pi = p + h • p_w • g

P2 = p - ciśnienie na powierzchni równe ciśnieniu atmosferycznemu Po podstawieniu mamy:

(p + h • p_w • g) • T2 = 3 • p • Ti p • T2-+-h • p_w • g • T2 = 3 • p • Ti h • p_w • g • T2 = 3 • p • Ti - p • T2    /: pw • g • T2

h =

p • (3 • Ti - T2)

pw • g • T2

h =

h =

Jednostki:

p • (3 • ti + 3 • 273K -12 - 273K)

P • (3

pw • g • (t2 + 273K) ti -12 + 546K)

Pw • g ■ (t2 + 273K)

[h] =

[h] =

PaK

M IR rrf* s? JV rrf_

.kg

Pa = Nm

K

M I    ^m

^N=^k9ć

m² • s²

kg

, m

⁹1 kg

ł

- m

h =

m² • s² 100000-(3

17- 17 + 546)

55000

1000 • 9,81 • (17 + 273)    ^- 9,81 • 290

= 19/77

Odp.: Głębokość jeziora wynosi 19 metrów.

Zadanie 569 str.113

Dane:    Szukane:

h, S, p, m, p, g, R T = ?

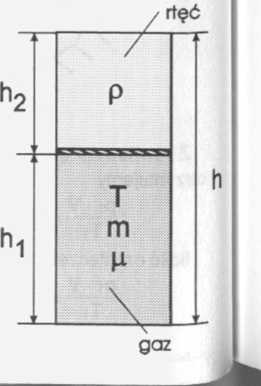
Aby rtęć nie była wypychana przez gaz jej ciśnienie hydrostatyczne ph musi być większe od ciśnienia p wywieranego na tłok przez gaz.

Ph>P

Ph = h2-pg,    ale    h2 = h-hi

stąd ph = (h - hi) • p • g Z równania Clapeyrona otrzymamy:

p-^ = ^m-R

P-V =

T P

m- R -T

/•T

/: V

P =

stąd p =

P

m- R T P-V ' m- R -T

gdzie

V = S- hi

P • S • hi

Ponieważ ph > p, więc po podstawieniu mamy:

(h-hi)-p • g > ™    ^ /-p-S-hi

(h-hi)-hi-p-S-p-g>mRT /:m-R

T<(h-h₁)-h,-^>l'g'P'⁹ m • H

Wykreślamy zależność temperatury gazu T od wysokości hi

T = (h - hi) • hi

P-Spg m • R

Wykresem jest parabola przyjmująca wartości zero dla hi = 0 i h2 = h

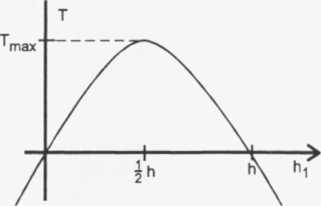
Z wykresu widzimy, że największą wartość temperatury Tmax dla stanu równo-

1 .

wagi cismen gaz osiąga przy hi = - h i wówczas mamy:

t    h h P- S • p • g

Tmax (h ₂)-₂- _{m R}

t _ h h p. • S • p • g ^max ' 2 ’ 2 ' m ■ R

_ h² • p - S • p • g ^Tmax 4 • m • R

Odp.: Rtęć nie będzie wypychana przez gaz dla temperatury określonej

wzorem Tmax =

h² • p S • p ■ g 4 • m • R