Image38 (16)

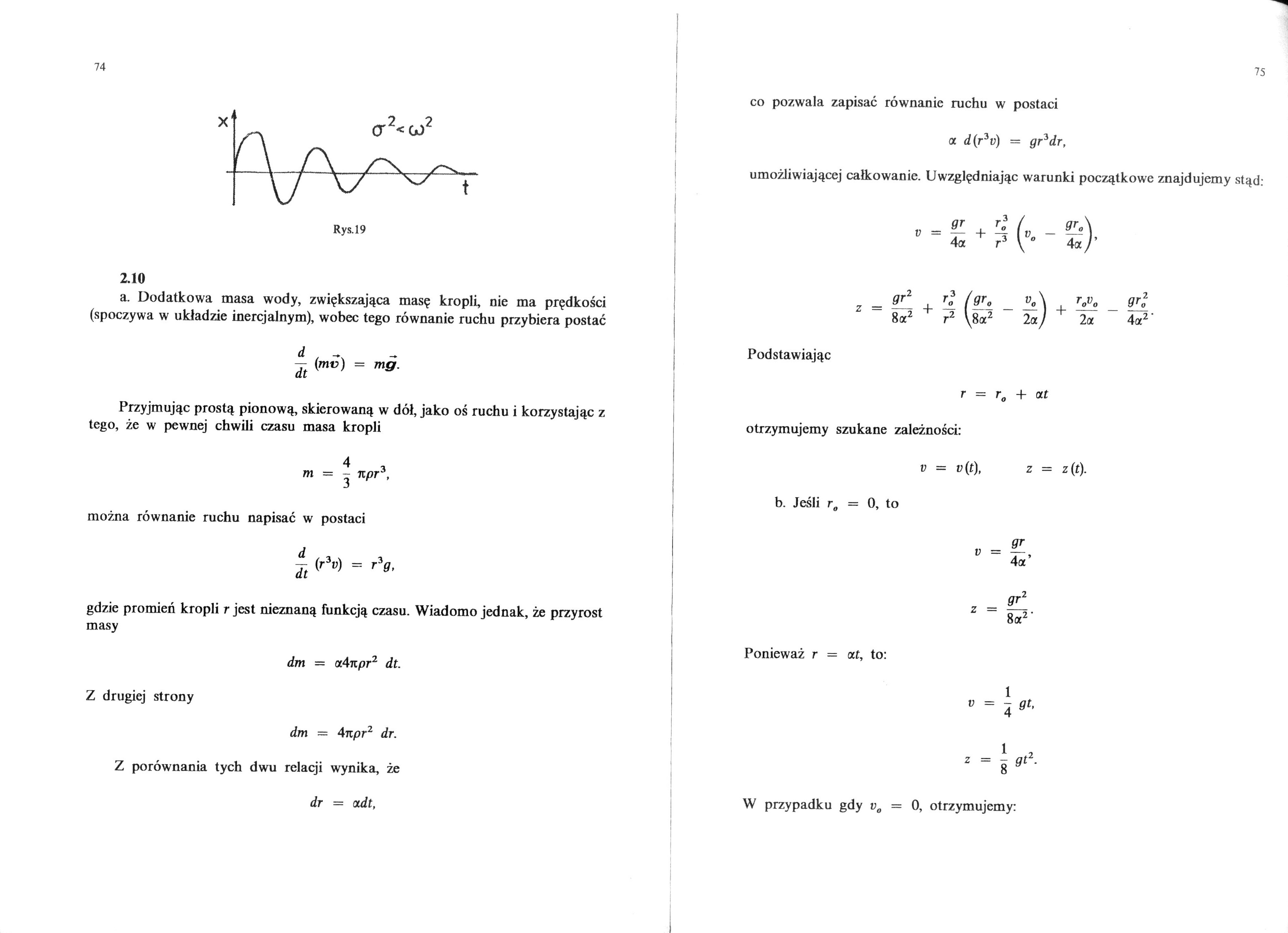
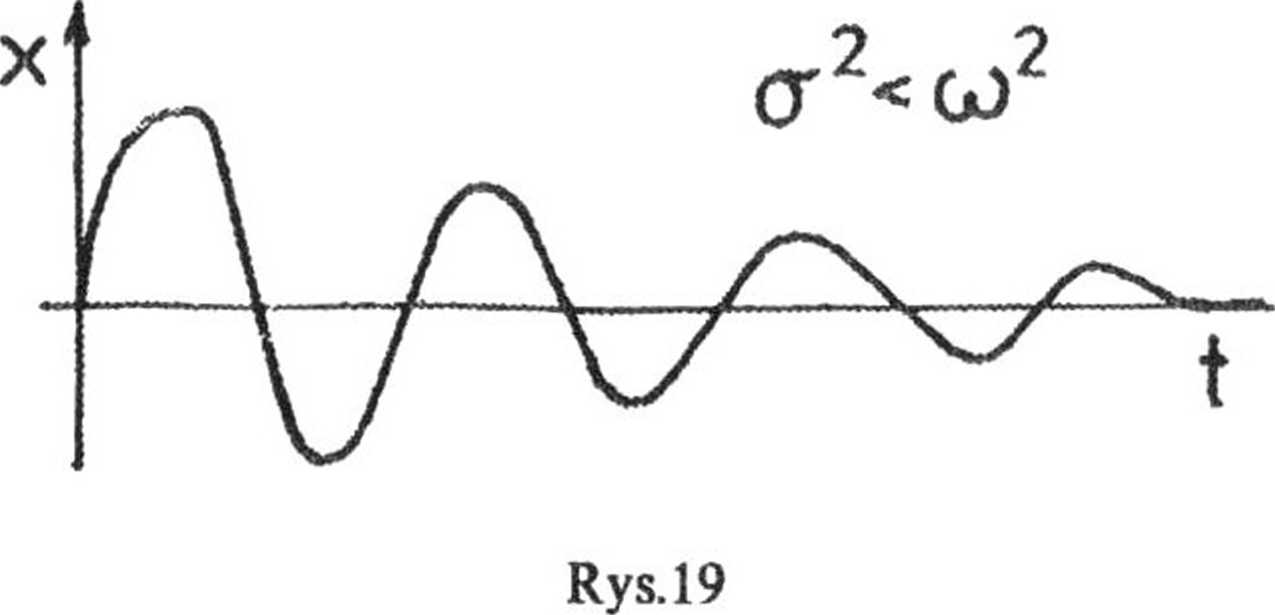
74

2.10

a. Dodatkowa

asa wody, zwiększająca masę kropli, nie ma prędkości

(spoczywa w układzie inercjalnym), wobec tego równanie ruchu przybiera postać

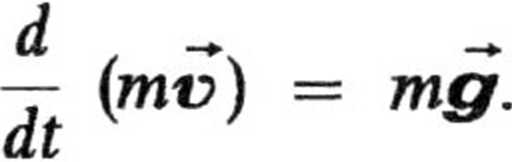
Przyjmując prostą pionową, skierowaną w dół, jako oś ruchu i korzystając z tego, że w pewnej chwili czasu masa kropli

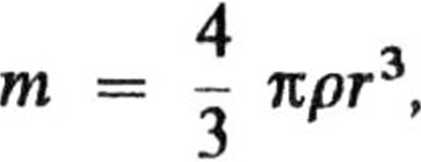
można równanie ruchu napisać w postaci

d

7t

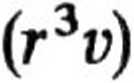
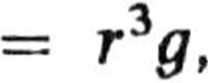
gdzie promień kropli r jest nieznaną funkcją czasu. Wiadomo jednak, że przyrost masy

dm = cc4npr² dt.

Z drugiej strony

dm = 4npr² dr. Z porównania tych dwu relacji wynika, że

dr = a dt,

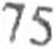
co pozwala zapisać równanie ruchu w postaci

ot d(r³v) = gr³dr,

umożliwiającej całkowanie. Uwzględniając warunki początkowe znajdujemy stąd:

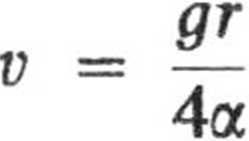
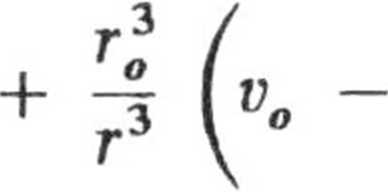
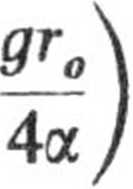
5

ąr²    rj igr„v„\    r„v₀

8a²    r² \8a² lot)    2ct    4a²

Podstawiając

r = r_Q + ott

otrzymujemy szukane zależności:

V = v(t),    z = z(t).

b. Jeśli r_a = 0, to

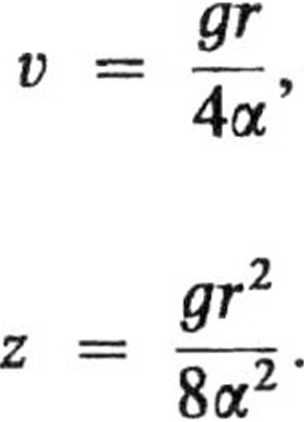
Ponieważ r = ott, to:

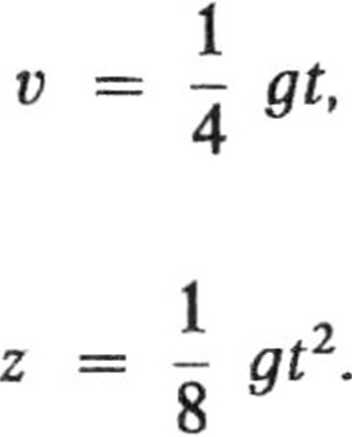
W przypadku gdy v_a 0, otrzymujemy: