Image9 (40)

72

Rozwiązania zadań ze zbioru "MENDLA"

Dla przemiany izotermicznej gazu zawartego w strzykawce otrzymamy: pi • Vi = p2 • V2, gdzie pi = P i Vi = V Ciśnienie P2 w strzykawce jest sumą ciśnienia atmosferycznego p = pi oraz nienia hydrostatycznego ph = h p g na głębokości h.

P2 = p + hpg

Wyznaczamy V2:

V2 = I2 • S,

V₂ = (I - Al) • S ,

ale

lecz

l₂ = I - Al V = l- S

/: S

• s

v₂ = ||-ai

V₂ = V - Al • s

Znając p₂ i V2 możemy je podstawić do wzoru:

p • V = P2 • V₂

stąd p • V = (p +h • p • g) • (V-Al • S)

Z ostatniej zależności, po przekształceniu wyznaczamy Al.

pV = pV + h- pgV-pAlS-hpg-AlS

p-Al-S + hpg-AlS = hp-gV

Al • S(p + h • p • g) = h • p • g • V /: S • (p + h ■ p • g)

AU hpg.y S (p + h p - g)

Al =

3 m ■ 1000^ • 10^- 0,00002^ _rrr sr_

0,0001 nł • (100000Pa + 3m- 1000^- 10^)’

rrr sr

Pamiętamy, że

I ^m A/

^k97 ^{= N}

Pa-J±

^a~nł

Al =

0,6m- N

Al =

0,0001 m² ■ (100000— + 30000-^) nr    rrr

0,6N ■ m

0,0001 nł • 130000-^ rrr

Al =

0,6/V- m

13 N

Al « 0,042m = 4,2cm

Odp.: Tłok strzykawki przesunął się o 4,2 cm.

Rozwiązania zadań ze zbioru "MENDLA

73

Zadanie 587 str.117

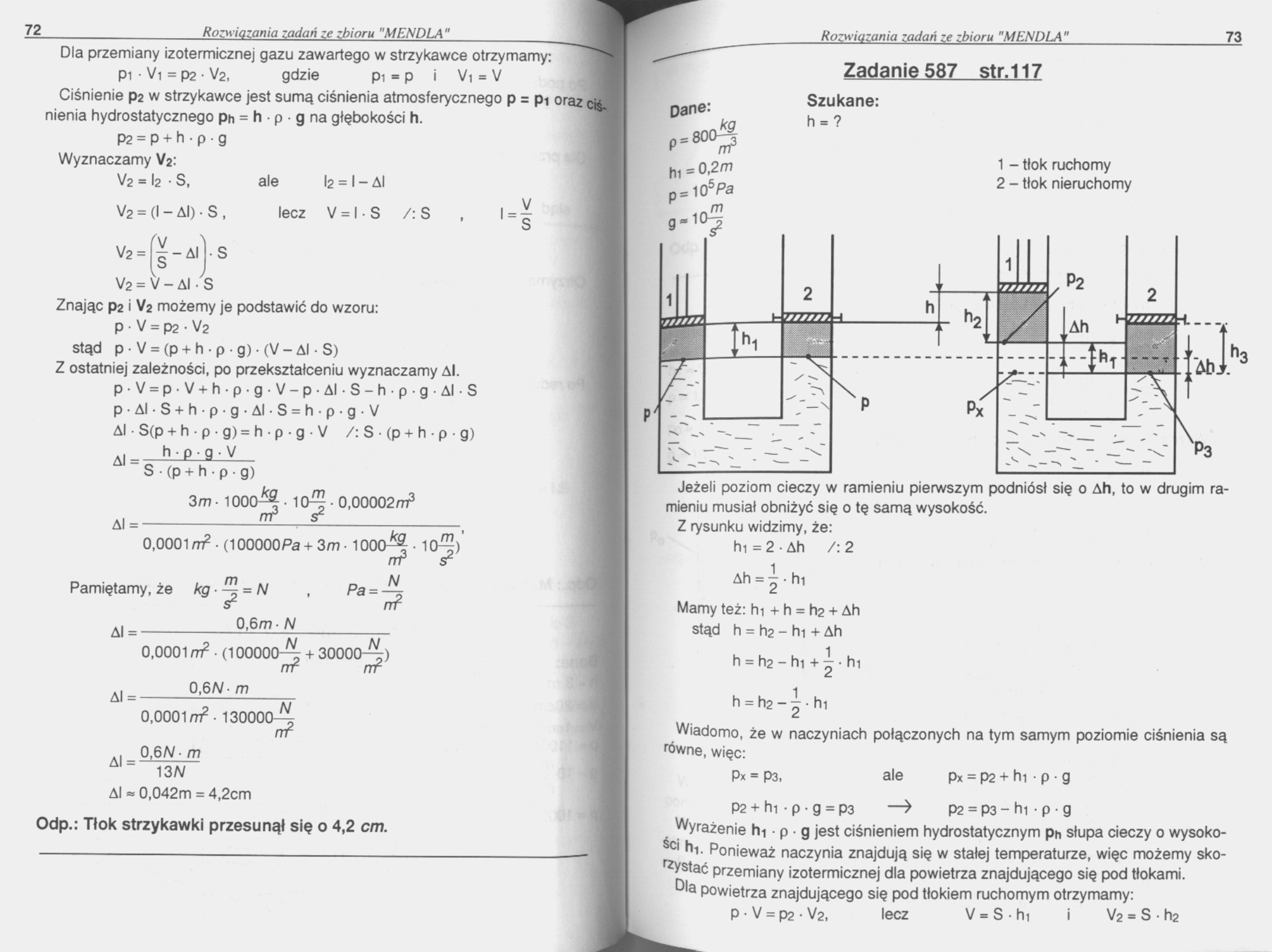
1    - tłok ruchomy

2    - tłok nieruchomy

Jeżeli poziom cieczy w ramieniu pierwszym podniósł się o Ah, to w drugim ramieniu musiał obniżyć się o tę samą wysokość.

Z rysunku widzimy, że:

hi = 2 • Ah /: 2

Ah=i-h,

Mamy też: hi + h = h2 + Ah stąd h = h2 - hi + Ah

h = h2 - hi + ^ • hi h = h2 - ^ ■ hi

Wiadomo, że w naczyniach połączonych na tym samym poziomie ciśnienia są równe, więc:

Px = P3,    ale px = P2 + hi • p • g

P2 + hipg = p3    —>    p2 = P3-hi-p-g

Wyrażenie hi • p g jest ciśnieniem hydrostatycznym ph słupa cieczy o wysokości hi. Ponieważ naczynia znajdują się w stałej temperaturze, więc możemy skorzystać przemiany izotermicznej dla powietrza znajdującego się pod tłokami.

Dla powietrza znajdującego się pod tłokiem ruchomym otrzymamy:

p . V = p2 • V2, lecz    V = S • hi i V2 = S • h2