img047 (27)

Można więc dokonać następnego rozdzielenia

1 d¹    i

— Ar-O = -m²,    (II-16)

^ dcp~ a

<t> = B\cosm(p+B2 smm(p,    (II-17)

lub też:

O = #|exp(/mę?)+ #₂exp(-.//w<p).    (11-18)

Ze względu na okresowość kąta (p, m. musi być liczbą całkowitą.

Dla R pozostaje równanie

dr

^-) + (k²r² -m²)? = 0,

2? . , _# lub po podzieleniu przez k r i wprowadzeniu współrzędnej bezwymiarowej

Ź=kr.    (11-19)

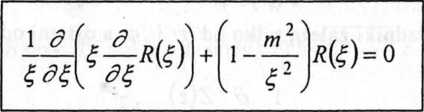
(11-20)

Jest to jedno z najbardziej znanych równań fizyki matematycznej tzw. równanie Bessela. Jego rozwiązaniem jest kombinacja liniowa dwóch różnych liniowo niezależnych funkcji tzw. funkcji cylindrycznych, które można wybrać w różny sposób. Para tych funkcji składa się z tzw.funkcji Bessela J_m(^) = J_m(kr) i z tzw.funkcji Neumanna N_m(g)= N_m(kr), tzn.

R(r) = C_lJ_m(kr) + C₂N_m{kr)

Przy rozdzielaniu zmiennych można postąpić również w inny sposób

1 d²

= -*²,

tak, że: jak również:

z dl² Z - A i cos kz + A 2 sin kz,

Z = A^exp(j kz)+ Z₂exp(- j kz).

(11-22)

(11-23)

(U-24)

Otrzymuje się wtedy równanie na R ze zmienną bezwymiarową

(H-25)

rj=jkr,

również w postaci równania różniczkowego Bessela

\_d__

nćn

^dr)

1-

m

R(v)= 0

z rozwiązaniem

R{r)=C_]J_m(jkr)+C₂N_m{jkr)

(11-26)

W zależności od rodzaju problemu ustala się, który ze sposobów rozdzielania należy zastosować. W zasadzie obydwa są równoważne. Można też zawsze przejść z jednego sposobu do drugiego podstawiając za k, jk lub na odwrót. Dla zadań gdzie rozwiązanie zależy od z, k— 0. Ten przypadek szczególny prowadzi do elementarnej funkcji R(r). Funkcje J_m{kr), N_m(kr) mają w zasadzie inne

właściwości niż funkcje J^jki'), N_m(jkr). Argument (jkr) pojawia się często wtedy, gdy wprowadzane są zmodyfikowane funkcje Bessela.

Zmodyfikowana funkcja Bessela pierwszego rodzaju zdefiniowana jest wzorem

I_m(x)=r^mJ_m((11-27)

a zmodyfikowana funkcja drugiego rodzaju

(11-28)

(11-29)

\J_m0*) + J^Nm0'*)]•

Rozwiązanie ogólne można podać wtedy w postaci

R(_r) = C_lI_m(kr)+C₂K_m{kr)

Należy przy tym dodać, że dla specjalnych typów zadań stałe mogą być wybrane w inny sposób (np. jeżeli zadany jest potencjał ę> = const na powierzchni). Należy przy tym zauważyć tylko, że m nie musi być wtedy liczbą całkowitą. Poniżej przedstawiono niektóre ważniejsze własności funkcji cylindrycznych. Istnieje bogata literatura w której zestawiono różnorodne własności tych funkcji [3,4,16,17].