img429 (2)

Analogicznie postępujemy w przypadku drugiej granicy. Tym razem jednak x—>+oo, więc | x | - x. Mamy zatem

lim

x²- 1

= lim

x—>+oo    2    -| x->+oo

|x|\1 + \

1 ^x

+00 j.

t T

= lim -

X->+00

X- V1 +

X²

= lim

X—>+00

= +00.

1 +

1

Ad b)

+00

t

+00

t

lim [-Vx² + x + 4 - V x² + 7

X—+-00\

₌ |_im (VX² + X + 4 - V X² + 7 ) (Vx²~+ x + 4 + V x² + 7 ) ^x-~°    V x² + x + 4 + Vx² + 7

—00

t

= |_im [(x² + x + 4) - (x² + 7) l _

lim

x - 3

x-^°_A/x² + x + 4 + Vx² + 7    V x² + x + 4 + V x² + 7

lim

X->-00

'1- 3"

x

	7				i	(	\
X^2	1 +	1 +	4	+ 1	J X^2	1	+ 4
		X	x^2J				X^2J

I

+oo

= lim

X—^—co

Ul

1 + - + 4 + "V1 +

x x²

Putlobnle obliczamy

Hm (s/x² + x + 4 - s/ x² + 7

X >+oo\

	1	3 X
X-++oo	h + ! + X	4 + y x^,L	x^d

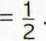
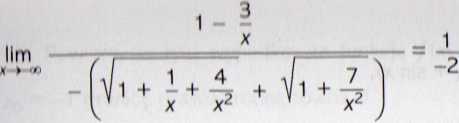
PR/YKIAD B.

sin x „ . .. sin x _ _

Wykapmy, ze lim-= 0 i lim —--0.

⁷    x-*-00 X    X-++CC X

| )o dowodu wykorzystamy twierdzenie o trzech funkcjach. Sformułowaliśmy je dla granicy funkcji w punkcie, ale można wykazać, że jest ono również prawdziwe dla granic funkcji w - qo oraz w +co.

Nlnch będzie x > 0. Wobec tego, że

-1 < sin x < 1.

mamy

_ 1 < sin x _< 1_

X X - X

Ponieważ lim

X—>+oo

= lim -

x->+°o X

O, więc z twierdzenia o trzech funkcjach wynika, że

,. sin x _ lim -= O.

x-»+oo x

Inżeli natomiast x < O, to z nierówności -1 < sin x < 1. wnioskujemy, że

_ 1 > ^s'^{n x} > 1 x x x'

skąd w drodze analogicznego rozumowania wynika, że lim

sin x

x

= O.