img036 (47)

^6

tych cs zasadzie prostych pomocniczych, to możemy zadanie rozwiązać za pomocą dwóch punktów ponocnioayah C i D, obranyoh po obydwu stronach proste j AB (rys. 28). Otrzymamy dwa trójkąty pomocnicze AA CM t ABD1, w których pomierzymy kąty a i /5 oraz długośol AC « a, CD = b i DB e c* Jeżeli obliczymy bok C1 «= x, to wyznaczymy punkt pośredni 1 na prostej AB, U tym celu możemy ułożyć dwa równania sinusów dla obydwu trójkątów* Szczegółowe rozwi^zraie tych zadań znajdzi* czytelnik w pracy £163«

T 5 c r. f^s n i o punktu przecięcia się dwóch prost2ch» Do wyznaczenia w terenie punktu przecięcia się prostych AB i CD (ryso 2$) pctrzabc dwóab obserwatorów, jednego pomocnika oraz 5 tyczek. Po ust&ęicals tyczek w punktach i, E, C i I obserwatorzy ustawia**

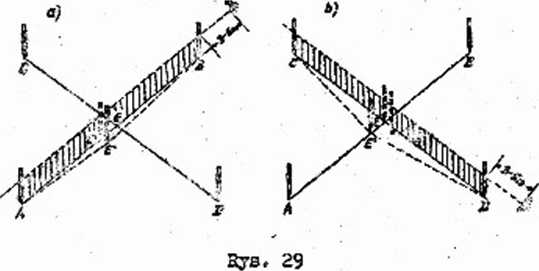
ją się w odległości 5 - j? m od punktów B i D, zaś pomocnik ustawia się z piątą tyczką w przybliżeniu na. przecięciu cię wspomnianych prostych w punkcie B\ Obserwator w punkcie B ustawia pomocnika ua proste j AE w punkcie B" (rys. 29a)_t & naetępnio obserwator w punkcie D ustawia tegoż pomocniku na prostej CD w punkcie E**' (rys, 29b). Jeż6li na skutek poruszenia się pcdJoonJfco v ohwili ustawiania go przos obserwatora w punkoio D tyczka E zostanie usunięta z prostej AB, jak na rysunku 29h, to wóv/czas obs*rws_tyo£ vt punkcie B musi ją na nowo pprowadzić ca prostą AB, Czynność powyższą powtarzają obserwatorzy B i 3 tak długo, aż tyczka zajmie takie położenie S. źe-zna jdzie się równocześnie na prostej AS i CD. Punkt B będzie wtedy punktem przecięcia się prostych AE 1 CB_fi Przy pewnej <ępiavrte zespołu obaj obserwatorzy powinni podawać rówsooześnie swoje znaki pomoce mikowi.

2.1.2* Pyczenle kątć'/; stałych 90^C 1 180°

Tyczenie kąta za pomocą taśmy, Wytyczenia •prostopadlej CT do prostej AB w punkcie C wykonujemy w następujący sposób. Ns prostej AB odmierzamy cd punktu C w kierunku do A i do 3 tę samą licz-