300 (18)

600 24. Obwody nieliniowe prądu stałego

a drugiego liniowego) można to zagadnienie rozwiązać za pomocą metody przecięcia charakterystyk przedstawionej na rys. 24.9. W układzie współrzędnych /, U rysujemy charakterystykę elementu 7. Na osi I odkładamy odcinek 00' = /, a następnie w układzie współrzędnych /', V rysujemy charakterystykę elementu 2. Rozwiązanie zagadnienia daje punkt A przecięcia się charakterystyk. Rzut punktu A na oś U wyznacza napięcie U na połączeniu, a rzut punktu A na oś / dzieli prąd / = 00' na prądy I₂.

Opisane metody wyznaczania charakterystyki łącznej, połączenia szeregowego i równoległego pozwalają znaleźć charakterystykę połączenia szeregowo-równoleg-łego elementów nieliniowych (rys. 24.10). W tym celu znajdujemy najpierw charakterystykę łączną połączenia równoległego elementów 2, 3. Następnie wykorzystując znalezioną charakterystykę oraz charakterystykę elementu 7, wyznaczamy charakterystykę całego połączenia.

24.4. Obwody zawierające jeden element nieliniowy

W wielu praktycznych zagadnieniach występują obwody, zawierające tylko jeden element nieliniowy. Obliczanie takich układów wydatnie upraszcza się przy wykorzystaniu twierdzenia Thevenina.

Niech A, B oznaczają zaciski elementu nieliniowego. Część obwodu zawierającą wyłącznie elementy liniowe przedstawiamy w postaci dwójnika aktywnego o zaciskach A, B. W związku z tym rozpatrywany obwód przybiera postać jak na rys. 24.11.

A I

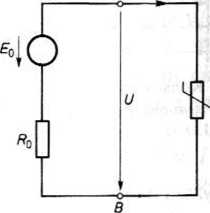
Rys. 24.11. Schematyczne przedstawienie obwo- Rys. 24.12. Przekształcony obwód z rys. 24.11 du zawierającego jeden opornik nieliniowy

Na podstawie twierdzenia Thevenina możemy dwójnik aktywny zawierający elementy liniowe przedstawić w postaci źródła energii. Napięcie źródłowe E₀ tego źródła równa się napięciu między punktami A, B przy przerwanej gałęzi A, B\ rezystancja wewnętrzna R₀ tego źródła równa się rezystancji dwójnika między punktami A, B, jeśli usunięte są wszystkie źródła energii. Układ z rys. 24.11 przedstawimy w postaci jak na rys. 24.12.

Napięcie U na elemencie nieliniowym równa się napięciu między zaciskami A, B źródła energii, czyli

U = E₀ — R₀I.    (24.1)

Obliczenie prądu / oraz napięcia U sprowadza się do rozwiązania układu dwóch równań z dwiema niewiadomymi U, I. Jednym równaniem jest wyrażenie (24.1), a drugim — charakterystyka U(I) elementu nieliniowego podana w postaci graficznej. Ten układ równań rozwiązujemy graficznie. W tym celu rysujemy charakterystykę elementu nieliniowego w układzie współrzędnych /, U (rys. 24.13),

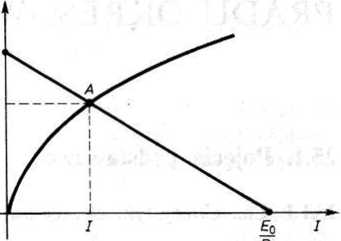
u £o

u o

Rys. 24.13. Wyznaczenie prądu w obwodzie z rys. 24.12

a następnie rysujemy prostą U = E₀ — R₀I. Współrzędne punktu A przecięcia się tej prostej z charakterystyką elementu nieliniowego określają napięcie U oraz prąd /. Znając prąd / oraz napięcie U elementu nieliniowego, możemy wyznaczyć rozpływ prądu w pozostałej części układu.