308 (17)

616 25. Obwody nieliniowe prądu okresowego

Podstawiając t/t =    sin («t do tego wyrażenia, otrzymujemy

i = a₁i/r_msina»t + a₃i/r^sin³a)r.

Wykorzystując tożsamość trygonometryczną dla sin³ cot daną wzorem (25.6) znajdujemy i = /_mlsincot-/_m3sin3cot, przy czym

Stwierdzamy zatem, że krzywa prądu w uzwojeniu cewki zawiera pierwszą i trzecią harmoniczną. Gdy cot = re/2, wówczas prąd przybiera wartość maksymalną równą I_mi +/_m3, większą od wartości maksymalnej I_ml harmonicznej podstawowej. Tłumaczy to zaostrzenie krzywej prądu w uzwojeniu cewki.

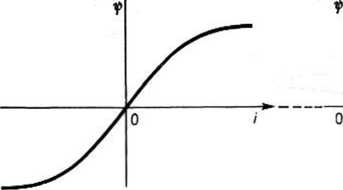
Rysunek 25.21 przedstawia konstrukcję przebiegu strumienia skojarzonego i/' przy sinusoidalnym prądzie w uzwojeniu cewki. Stwierdzamy, że krzywa strumienia skojarzonego ulega spłaszczeniu.

%

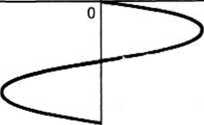
Rys. 25.21. Konstrukcja przebiegu strumienia skojarzonego przy sinusoidalnym prądzie w uzwojeniu cewki z rdzeniem stalowym

Gdy w uzwojeniu rozpatrywanej cewki płynie prąd sinusoidalny i = I_m sin cot, wówczas wygodniej jest korzystać z wyrażenia \p = b_li—b₃i³, przy czym b_t, b₃ są współczynnikami stałymi. Podstawiając i = I_msino)t do tego wzoru i dokonując podobnych przekształceń jak poprzednio, znajdujemy

sin cot+i/r_m3sin3cof,

przy czym

Stwierdzamy zatem, że krzywa strumienia magnetycznego zawiera pierwszą i trzecią harmoniczną.

Wartość maksymalna strumienia skojarzonego występuje w chwili, gdy cot — n/2 i wynosi    co tłumaczy spłaszczenie krzywej. Krzywa strumienia jest

anty symetryczna, wobec tego zawiera wyłącznie harmoniczne nieparzyste.

Gdy prąd w uzwojeniu cewki jest sinusoidalny, wówczas napięcie na tym uzwojeniu jest odkształcone; mamy bowiem

cos 3 cot.

dt/t

u = — = cos cot + 3o^_m3

Na tej podstawie wysnuwamy wniosek, że krzywa napięcia na zaciskach uzwojenia cewki zawiera tylko harmoniczne nieparzyste, wskutek czego jest antysymetryczna.

Stwierdziliśmy, że nieliniowa charakterystyka cewki z rdzeniem stalowym powoduje odkształcenie wielkości sinusoidalnych, wskutek czego występują okresowe wielkości niesinusoidalne. Jak wiadomo, funkcje okresowe można przedstawić w postaci szeregu Fouriera, będącego sumą nieskończenie wielu harmonicznych. W dalszych rozważaniach uwzględnimy tylko pierwszą harmoniczną (o najniższej częstotliwości), a pominiemy wszystkie wyższe harmoniczne. W tych warunkach będziemy mieli do czynienia z wielkościami sinusoidalnymi, wobec tego cewkę z rdzeniem stalowym można traktować jako element warunkowo nieliniowy.

Założenie to upraszcza wydatnie obliczanie prądów i napięć w obwodach zawierających cewki z rdzeniem stalowym, bowiem można stosować metodę liczb zespolonych oraz wykresy wskazowe. Wskutek tego otrzymuje się przejrzysty obraz zjawisk.

Na rysunku 25.22 podany jest wykres wskazowy cewki z rdzeniem stalowym. Na rysunku tym uwzględniono, ze prąd / jest w fazie ze strumieniem cf)_m i opóźnia się

U

I=U

0

Z.m

Rys. 25.22. Wykres wskazowy cewki z rdzeniem stalowym przy założeniach

upraszczających w fazie o kąt 90° względem napięcia U na zaciskach cewki. Omawiany wykres wskazowy dotyczy cewki z rdzeniem stalowym o pomijalnie małej rezystancji uzwojenia; ponadto nie uwzględniono histerezy magnetycznej i prądów wirowych.

W wyniku przyjętych założeń rozpatrujemy tylko jedno z trzech zjawisk towarzyszących zawsze prądowi elektrycznemu, a mianowicie istnienie pola magnetycznego. Z tego powodu rozpatrywany prąd nazywany jest prądem magnesującym i oznaczany symbolem /„.