324 (17)

648 25. Obwody nieliniowe prądu okresowego

U)t

U)t

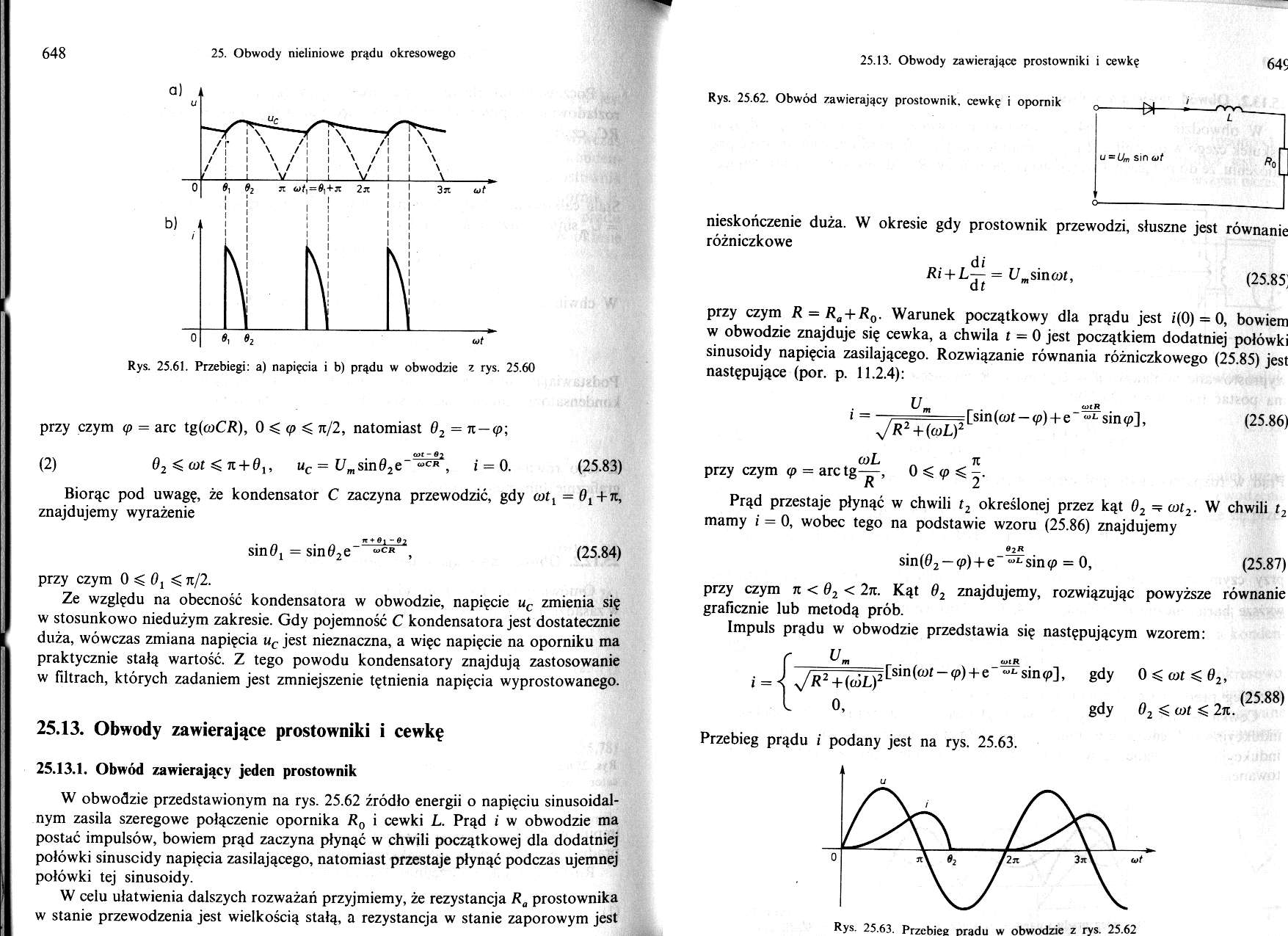
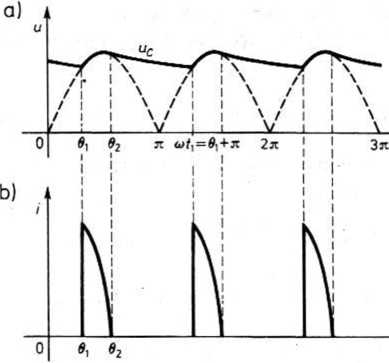
Rys. 25.61. Przebiegi: a) napięcia i b) prądu w obwodzie z rys. 25.60

przy czym <p = arc tg(a>CR), 0 ^ q> < ti/2, natomiast 0₂ = n — ę;

<ot ~

(2)    0₂ ^ cot < ji + 0,, u_c - l/_msin0₂e^{_ wCR} , i = 0.    (25.83)

Biorąc pod uwagę, że kondensator C zaczyna przewodzić, gdy cot_l =0_l+n, znajdujemy wyrażenie

sinO_Ł = sin0₂e~ «« ²,    (25.84)

przy czym 0 ^ Oj < Jt/2.

Ze względu na obecność kondensatora w obwodzie, napięcie u_c zmienia się w stosunkowo niedużym zakresie. Gdy pojemność C kondensatora jest dostatecznie duża, wówczas zmiana napięcia u_c jest nieznaczna, a więc napięcie na oporniku ma praktycznie stałą wartość. Z tego powodu kondensatory znajdują zastosowanie w filtrach, których zadaniem jest zmniejszenie tętnienia napięcia wyprostowanego.

25.13. Obwody zawierające prostowniki i cewkę

25.13.1. Obwód zawierający jeden prostownik

W obwodzie przedstawionym na rys. 25.62 źródło energii o napięciu sinusoidalnym zasila szeregowe połączenie opornika R₀ i cewki L. Prąd i w obwodzie ma postać impulsów, bowiem prąd zaczyna płynąć w chwili początkowej dla dodatniej połówki sinusoidy napięcia zasilającego, natomiast przestaje płynąć podczas ujemnej połówki tej sinusoidy.

W celu ułatwienia dalszych rozważań przyjmiemy, że rezystancja R_a prostownika w stanie przewodzenia jest wielkością stałą, a rezystancja w stanie zaporowym jest

Rys. 25.62. Obwód zawierający prostownik, cewkę i opornik

nieskończenie duża. W okresie gdy prostownik przewodzi, słuszne jest równanie różniczkowe

(25.85;

di

Ri + L— = U_ms\ncot, dr

przy czym R = R_a + R₀. Warunek początkowy dla prądu jest i(0) = 0, bowiem w obwodzie znajduje się cewka, a chwila t = 0 jest początkiem dodatniej połówki sinusoidy napięcia zasilającego. Rozwiązanie równania różniczkowego (25.85) jest następujące (por. p. 11.2.4):

i =

JR² + (coL)

a>tR

=[sin(a>r — <p) + e~ ^wL sin</>],

(25.86)

coL    n

przy czym ę = arc tg—, 0 < (p <

R    2

Prąd przestaje płynąć w chwili t₂ określonej przez kąt 0₂ =? wt₂. W chwili t₂ mamy i = 0, wobec tego na podstawie wzoru (25.86) znajdujemy

02 R

sin(0₂ — ę) + e " "^sin cp = 0,    (25.87)

przy czym n < 0₂ < 2n. Kąt 0₂ znajdujemy, rozwiązując powyższe równanie graficznie lub metodą prób.

Impuls prądu w obwodzie przedstawia się następującym wzorem:

i =

V_m

yj R² +(cóL)²

0,

[sin(a>r — <p) + e "^Łsin<p],

gdy

gdy

0 ^ cot ^ 0₂,

„    (25.88)

0₂^cot ^ 2n.

Przebieg prądu i podany jest na rys. 25.63.

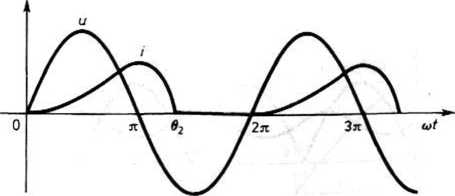
Rys. 25.63. Przebieg prądu w obwodzie z rys. 25.62