302 (19)

604 25. Obwody nieliniowe prądu okresowego

Przekaźnikiem idealnym nazywamy element nieliniowy opisany równaniem:

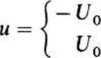
dla    i < 0,

dla    i > 0.

(25.3)

Charakterystykę przekaźnika idealnego przedstawia rys. 25.6.

Nieliniowymi obwodami rezystancyjnymi nazywamy obwody zawierające liniowe i nieliniowe oporniki, prostowniki lub przekaźniki idealne. Charakterystyki połączeń szeregowych i równoległych zawartych w obwodach rezystancyjnych znajdujemy przy zastosowaniu metod omówionych w p. 24.2 i 24.3.

W ogólnym przypadku charakterystyki elementów nieliniowych są nieliniowe zarówno dla wartości chwilowych, jak i dla wartości skutecznych. Istnieją jednak takie elementy, które mają charakterystykę nieliniową dla wartości skutecznych (lub maksymalnych), a charakterystykę liniową dla wartości chwilowych. Tego rodzaju elementy nazywamy elementami warunkowo nieliniowymi (p. 25.2).

25.1.2. Odkształcanie wielkości sinusoidalnych

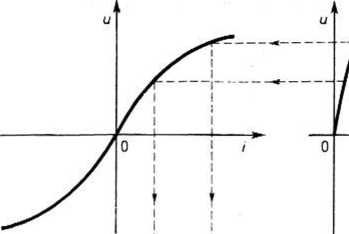
Cechą charakterystyczną elementów liniowych jest to, że nie zmieniają kształtu wielkości sinusoidalnych. Jeśli więc do zacisków elementu liniowego załączymy napięcie sinusoidalne, to w elemencie płynie prąd sinusoidalny i odwrotnie: przy przepływie prądu sinusoidalnego napięcie na zaciskach elementu liniowego jest sinusoidalne. Własności tej nie mają elementy nieliniowe. Aby się o tym przekonać, znajdziemy przebieg prądu w oporniku nieliniowym, gdy napięcie ma kształt sinusoidalny. Przebieg prądu wyznaczamy za pomocą konstrukcji przedstawionej na rys. 25.7 na podstawie charakterystyki elementu. Konstrukcja ta pozwala wyznaczyć

%

Rys. 25.7. Konstrukcja przebiegu prąciu w oporniku idealnym

r

25.1. Pojęcia podstawowe    605

kolejne punkty krzywej prądu i(cuf), odpowiadające poszczególnym punktom krzywej napięcia u(cut). Z rysunku 25.7 widzimy, że załączenie napięcia sinusoidalnego do elementu nieliniowego powoduje przepływ prądu niesinusoidalnego. Stwierdzamy zatem, że w elementach nieliniowych występuje odkształcenie wielkości sinusoidalnych.

W obwodach nieliniowych prądu zmiennego występuje wiele zjawisk, których nie ma w obwodach liniowych. Do zjawisk tego rodzaju należą: stabilizacja napięć i prądów, prostowanie prądów, wytwarzanie napięć różnego kształtu itd.

Obliczanie obwodów nieliniowych prądu zmiennego jest znacznie trudniejsze niż obwodów liniowych. Stosowane są metody graficzne, analityczne i numeryczne. Metody graficzne są poglądowe i na ogół zapewniają wystarczającą dokładność do celów praktycznych. W metodach analitycznych wykorzystuje się wzory aprok-symujące charakterystyki elementów nieliniowych; metody te są zazwyczaj mało dokładne, ale zaletą ich jest to, że umożliwiają otrzymanie ogólnych zależności między wielkościami. Metody numeryczne zapewniają dużą dokładność obliczeń i mają coraz większe znaczenie ze względu na zastosowanie elektronicznych maszyn cyfrowych.

W dalszych rozważaniach przedstawimy podstawowe metody obliczeń obwodów nieliniowych prądu zmiennego, znajdujących się w stanie ustalonym.

25.2. Elementy warunkowo nieliniowe

Jak wiadomo, elementami warunkowo nieliniowymi nazywamy elementy mające charakterystykę nieliniową dla wartości skutecznych, a charakterystykę liniową dla wartości chwilowych. Typowym przykładem elementu warunkowo nieliniowego są oporniki zwane termistorami.

Termistory mają rezystancję zależną w wyraźny sposób od temperatury, która z kolei zależy od wartości skutecznej prądu w elemencie. Oznacza to, że rezystancja termistorów zależy od wartości skutecznej prądu. Termistory mają stosunkowo dużą bezwładność cieplną, wskutek czego przy częstotliwościach większych od kilkudziesięciu herców zmiana temperatury w ciągu części okresu odpowiadającej wzrostowi prądu od 0 do wartości maksymalnej jest pomijalnie mała. W związku z tym można przyjąć, że przy przepływie prądu okresowego temperatura, a więc i rezystancja termistora jest wielkością stałą. Oznacza to, że termistor ma liniową charakterystykę dla wartości chwilowych, gdy wartość skuteczna prądu jest stała.

Przy zmianie wartości skutecznej prądu zmienia się temperatura, a więc również i rezystancja termistora. Oznacza to, że termistor ma nieliniową charakterystykę dla wartości skutecznych.

W celu znalezienia przebiegu prądu w termistorze przy znanym napięciu sinusoidalnym, wyznaczamy wartość skuteczną U napięcia i na charakterystyce U(I) zaznaczamy punkt A, odpowiadający wartości U (rys. 25.8). Prosta p poprowadzona przez punkty O, A jest charakterystyką liniową dla wartości chwilowych przy danej