303 (15)

606 25. Obwody nieliniowe prądu okresowego

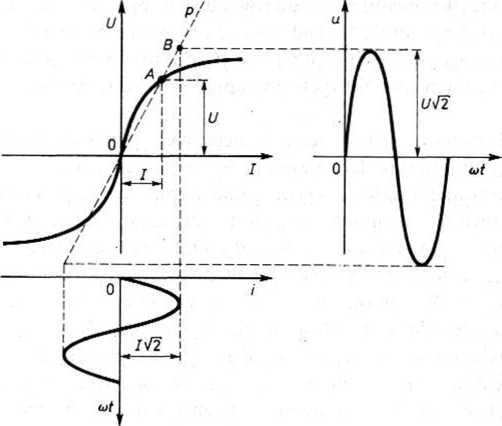
Rys. 25.8. Konstrukcja przebiegu prądu w termistorze

wartości skutecznej U = const. Wartość maksymalną prądu wyznaczamy, znajdując odciętą punktu B (rys. 25.8), odpowiadającego wartości maksymalnej U Jl napięcia na termistorze. Przy sinusoidalnym napięciu na termistorze prąd jest również sinusoidalny. Stwierdzamy zatem, że elementy warunkowo nieliniowe nie odkształcają wielkości sinusoidalnych.

Gdy zmieni się wartość skuteczna U napięcia, wówczas punkt A przesunie się i charakterystyka liniowa p, dla wartości chwilowych, będzie miała inne nachylenie.

Elementy warunkowo nieliniowe odgrywają dużą rolę w teorii obwodów nieliniowych, bowiem w wielu przypadkach można pominąć odkształcenie przebiegów sinusoidalnych spowodowane występowaniem elementów nieliniowych. Wobec tego w tych przypadkach można elementy nieliniowe traktować jak elementy warunkowo nieliniowe. Tego rodzaju postępowanie powoduje zawsze powstanie pewnego błędu, jednakże w wielu przypadkach jest on stosunkowo nieznaczny.

25.3. Aproksymacja charakterystyk nieliniowych

Charakterystyki elementów nieliniowych wyznacza się zazwyczaj doświadczalnie i przedstawia się w postaci graficznej. Przedstawienie otrzymanych krzywych za pomocą wzoru nazywa się aproksymacją charakterystyk.

Omówimy dwa rodzaje aproksymacji charakterystyk.

25.3.1. Aproksymacja za pomocą wielomianu

Charakterystykę i(u) elementu nieliniowego można przedstawić w otoczeniu punktu u = u₀ za pomocą wielomianu

i(u) = a₀ + a_l(u-u₀) + a₂(u-u₀)² + ...+a„(u-u₀)ⁿ,    (25.4)

przy czym współczynniki a₀, a,, a₂,..., a„ mają stałe wartości. Gdy u₀ = 0, wówczas otrzymuje się

i(u) = a₀ + a₁u + <j₂u² + ... +a_nuⁿ.    (25.5)

Na ogół posługujemy się wielomianami stopnia trzeciego.

Do zacisków elementu nieliniowego załączamy napięcie u = l/_msinwr. Aprok-symując charakterystykę tego elementu za pomocą wielomianu stopnia trzeciego, otrzymujemy

i = a₀ + ^ai C_msincof + a₂C²sin²mf + a₃C²sin³cot.

Wykorzystując wzory

(25.6)

(25.7)

sin²mt = -(1 — cos2cor), sin³cut = -(3sincut — sin3wt), 2    4

znajdujemy

i = I₀ + /_mlsino)t — l_m2cos2(ot — I_m3sin3ajl,

przy czym

1    ,    3

Jo =a₀ + -a₂Ui,    l_ml = a_lU_m + ~a₃Uⁱm,

1

2⁶²'

Im2 =

3

m •

(25.8)

Na podstawie tych wzorów wnioskujemy, że składowe stałe oraz amplitudy harmonicznych parzystych prądu zależą tylko od współczynników przy potęgach parzystych wielomianu aproksymującego charakterystykę. Natomiast amplitudy harmonicznych nieparzystych prądu zależą tylko od współczynników przy potęgach nieparzystych. Wnioski te mają charakter ogólny.

Powyższe wnioski zostały wyprowadzone na podstawie charakterystyki i(u) opornika. Jest rzeczą oczywistą, że podobne wnioski można otrzymać również dla cewki nieliniowej oraz kondensatora nieliniowego, opisanych odpowiednio charakterystykami q(u). Aproksymacja charakterystyki i/^(ij oraz i(ip) cewki nieliniowej za pomocą wielomianu omówiona będzie nieco szczegółowiej w p. 25.5.2.

Przykład 1. Charakteryslykę elementu nieliniowego aproksymowano za pomocą wielomianu i = 0,12 + 0,42u + 0,20u², przy czym prąd i wyrażony jest w ampcrach. a napięcie u w woltach. Do rozpatrywanego elementu doprowadzono napięcie u = 2sin<ur woltów. Obliczyć: a) wartość chwilową prądu, b) wartość skuteczną prądu, c) moc czynną elementu.