310 (15)

620 25. Obwody nieliniowe prądu okresowego

uzwojenia cewki jest wielkością stałą; we wzorze (25.28) z oznacza liczbę zwojów

cewki.

Zmienne w czasie strumienie magnetyczne $, </>₀ wzniecają w uzwojeniu cewki napięcia

u

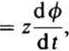
“o

d<£₀ _ di ² dt °d/

(25.29)

Na podstawie II prawa Kirchhoffa otrzymujemy dla obwodu z rys. 25.24 równanie

Ri + L₀— + ^un = ^u*    (25.30)

df

przy czym R oznacza rezystancję uzwojenia cewki.

Traktując cewkę z rdzeniem stalowym jako element warunkowo nieliniowy, przedstawiamy równanie (25.30) w postaci zespolonej:

{R+iaLJI+y^y,    (25.31)

a ponadto mamy

/ = /„ + /*-.    (25.32)

zgodnie ze wzorem (25.27). Zależności (25.31) i (25.32) są równaniami cewki z rdzeniem stalowym. Wartość skuteczna napięcia indukowanego w uzwojeniu cewki wskutek zmian czasowych strumienia głównego wyraża się wzorem (por. p. 9.9.2)

U, = 4,44 fz<f>_m,

gdzie /oznacza częstotliwość prądu w cewce, z — liczbę zwojów uzwojenia cewki, 4>_m — wartość maksymalną strumienia głównego.

&

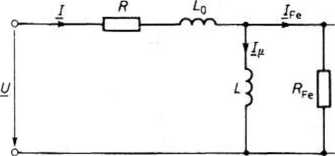
Rys. 25.25. Schemat zastępczy cewki z rdzeniem L_ stalowym

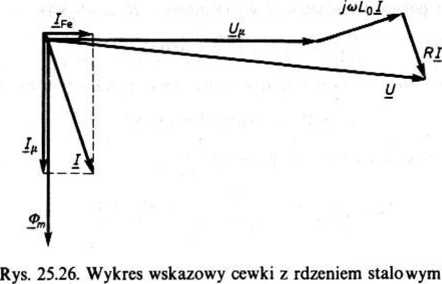
Równania (25.31) i (25.32) otrzymuje się na podstawie obwodu z rys. 25.25, zwanego schematem zastępczym cewki z rdzeniem stalowym. Na podstawie równań lub schematu zastępczego cewki z rdzeniem stalowym można narysować wykres wskazowy tej cewki (rys. 25.26).

W ogólnym przypadku elementy o parametrach R_he, L schematu zastępczego są nieliniowe i zależą od wartości skutecznej U_ft napięcia.

Schemat zastępczy cewki z rdzeniem stalowym ma ważne znaczenie, bowiem umożliwia obliczanie obwodów prądu sinusoidalnego zawierających cewki z rdze-

r

621

25.5. Cewka z rdzeniem stalowym

niem stalowym za pomocą metody liczb zespolonych. Otrzymane w ten sposób wyniki są oczywiście przybliżone, jednakże ich dokładność jest zazwyczaj wystarczająca dla celów praktycznych.

Przykład. Przy badaniu cewki z rdzeniem stalowym otrzymano wyniki następujące: wartość skuteczna napięcia na uzwojeniu U = 150 V, wartość skuteczna prądu w uzwojeniu / =0,72 A, moc czynna cewki P = 40,5 W, rezystancja uzwojenia R = 18 ft, reaktancja rozproszenia u>L₀ = 23 fl. Obliczyć: a) parametry R_ft, ioL schematu zastępczego cewki, b) wartość maksymalną strumienia magnetycznego w rdzeniu cewki, jeżeli liczba zwojów uzwojenia z = 450.

a) Moduł impedancji połączenia

U 150

Z = - = — = 208 n. /    0,72

Współczynnik mocy połączenia

P 40,5

cosę> = — = —-= 0,375,

Ul 150 0,72

czyli <p = 68°. Impedancja połączenia

Z = 208eⁱ⁶⁸‘ = (78+jl93)n.

Impedancja połączenia równoległego gałęzi zawierających elementy R_fe> coL (rys. 25.25) jest równa

Z' = Z—(R+jwL₀) = (60+jl 70) Cl.

Admitancja rozpatrywanego połączenia równoległego ma postać    .

1    1    60—jl70

“ ~Z'~ 60+jl70 ~ 60² + 170²

Biorąc pod uwagę, że admitancja połączenia równoległego gałęzi o elementach R_u, wL wyraża się

wzorem otrzymujemy

60² +170²

/?Fc “

60

= 542 a, oiL =

60² +170²

170

191 n.