JTDuda

Zestaw pytań do egzaminu z przedmiotu „Prognozowanie^i symulacje” Zarządzanie r.II

Model predykcyjny uzyskany metodą najmniejszych kwadratów daje miarodajne oceny rozkładu prawdopodobieństwa błędu prognozy jeśli:

a) został uzyskany na podstawie odpowiednio dużej liczby obserwacji

postać (struktura) modelu odwzorowuje z pomijalnym błędem faktyczną zależność stochastyczną zmiennej . objaśnianej y od zmiennych objaśniających X dla wartości X₀ dla których chcemy wyznaczyć prognozę y(X₀) c) jak w (b) i dodatkowo znany jest rozkład prawdopodobieństwa składnika losowego rh * jak w (b) i rozkład prawdopodobieństwa składnika losowego jest normalny

2. Zakreśl kody predyktorów (ARX-ARMAX; ARIX-ARIMAX; H-adaptacyjny Holta; T-trend minimalnokwadratowy;

ARX	ARlX /—S.	ET	TĄ	ZOP	ZOH
■ ^XR5		H	\.....	ŻOP	ZOH
ARX	AR!X		fj \ ■	ZOP .	feoi l'
	■ A RIX	H	•-r	ZOP ,'	ZOH
7vi?X	ARIX.	rtfr	0"	ZÓP	ZOH
ARX	\RIX	&	T	ZOP	ZOH
ARX	ARIX	fijj	^T J	£	ZOH

D -

'Z

a)

b)

c)

d)

e) 0 g)

U

może być zastosowany do prognozowania dowolnych szeregów; dla szeregów stacjon. daje jednokrokową prognozę o minimalnej dyspe; jego wyznaczenie nie wymaga dużej liczby danych (mniej niż 30); stosuje się tylko dla szeregów stacjonarnych; stosuje się dla szeregów niestacjonarnych;

szybko dostosowuje się do zmian właściwości statystycznych szeregu;

Jest łatwy do zastosowania i często uzasadniony (np.dla notow.giełdowych)

3. Mamy optymalny model ARMAX o postaci: j>„ =a-y_n_| +b-u_n_₃ +c-v„_₅ +d-z_n

z są proc.losowymi (E{z}=0). Jakie wartości przyjąć dla zmiennych y*, n\ v* i z (dopisz indeksy), aby obliczyć prognozę o minimalnej dyspersji i wskaż źródło danych (zakreśl kod: PO-pomiar; /^-prognoza; PL- wart.planowana arbitralnie).    *

,A *    •

' -V„łA

cr„ = cr_ I + d + a: ■    = cr.(l + d + a)^

a)    ₊1 = a • y_n<M +b-u_n._z + c• v_a^łrf-odchyl.stand, błędu prognoz^"wynosi: fcT'=cr.;

b) J>„_t6 = ° ■ y\tT+ b-u„^+c- T Yni(, P^PKJ PI. ; PO Ptf^PL

c)    współczynniki Wi>. c,    się:^lł)itralnie; metodą regresji liniowei^metoda minimalizacji błędu .prognozy

a_c = <j_z 5

O

1 ₊ d²:

R PL ; a_c = a.

+ d² +a<

n V

4.    Zastosowanie prognozy ZOH (podtrzymania wartości bieżącej E{y„ i}~y„ }jest formalnie uzasadnione, gdy:

£a) mamy zbyt mało danych, aby zastosować inny model;

|b) autokorelacja przyrostów szeregu jest statystycznie nieistotna;    .

Cf trafność prognozy nie ma znaczenia; d) szereg czasowy jest niestacjonarny;

5.    Przy małej liczbie danych historycznych (10-20) odpowiednim sposobem krótkoterminowego prognozowania szeregu czasowego może być:

aA ekstrapolacja trendu liniowego; b) wartość średnia elementów szeregu^^podtrzymanie zerowego rzędu ; model autoregresyjny; e) wieloczynnikowy model regresyjny

6.    Minimalno-kwadratowy model prognostyczny popytu na pewien towar daje prognozę punktową o wartości 1260 sztuk. Błąd prognozy ma rozkład normalny o dyspersji 50 sztuk. Dostawca wystawia do sprzedaży 1310 sztuk.

a)    Ryzyko wystąpienia braku towaru wynosi:

a) 5%; b 2.5%;    c) około 30%; (^cf^koło 15%; e) mniej niż 1%

b)    Oczekiwana liczba sprzedanych sztuk towaru wynosi:.,

a) około 1260; (jb) 1260; c) około 1310; cjfiieco mniej niż 1260; d) nieco mniej niż 1310

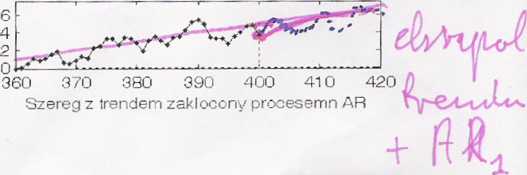
7.    Naszkicuj prognozy o minimalnym błędzie średniokwadratowym szeregów (do końca ramki):

'

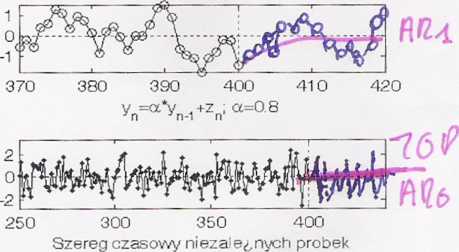
¹⁰ ' .a O n

O O o

22 20 18

250    300    350    400

Random walk

ZA(t

2

0

-2

-4

“TT

20

O 2    4    6    8    10    12    14

Dane kwartalne za 3 lata

250    300    350    400

Szereg okresowy z zakłóceniami niezależnymi