P1010785

202 J. FUNDAMENTY

13. Po wykonaniu fundamentów odbiór tych robót polegać powinien na sprawdzeniu zgodności z projektem: jakości użytych materiałów, usytuowania i wymiarów tych cle* mentów budowli. Odchylenia w poziomach górnej powierzchni podłoża, przygotowanej pod wykonanie fundamentów, mogą wynosić +20 mm przy fundamentach, których najmniejszy bok nie przekracza 4,0 m. Odchylenia w wymiarach fundamentów w planie mogą wynosić najwyżej +0,5%, przy czym nie mogą przekraczać 40 mm. Odchylenia w wymiarach elementów pionowych fundamentu nie mogą wynosić więcej niż +0,5%, przy czym nie mogą przekraczać 30 mm. Odchylenia poziomów powierzchni górnej fundamentów, mających być oparciem dla słupów stalowych lub żelbetowych prefabrykowanych, mogą wynosić +2 do 3 mm. Odchylenia w przesunięciu z osi takich fundamentów nie mogą wynosić więcej niż +3 do 4 mm.

Rysunki rzutów fundamentów powinny być starannie zwymiarowane w odniesieniu do osi słupów bądź ścian, aby uniknąć błędów montażowych.

Przykład 25. Obliczyć pasmo fundamentowe obciążone jak na rysunku poniżej.

Dane: długość belki /=15,0 m, dopuszczalne naprężenie na grunt £,=1,80 kO/cm¹, ciężar własny gruntu 7=1,85 T/m*, współczynnik podatności podłoża r=8,5 kG/cra*.

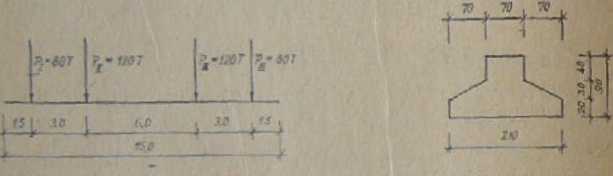
Rys. 3,35. Schemat statyczny lawy fiu da matowa] obcisło-    Rys. 3.36, Praskfdj lawy fuadsmeatowcj

ooj iytPdryca>e datmi łkani ikupiooynu_

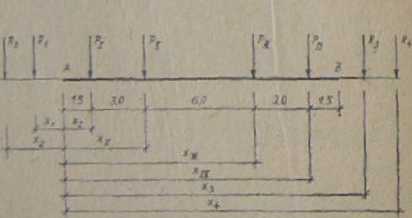
Rys. 3.37. Schemat obliczeniowy dla p. A lawy fuadameatowcj obdgiooej czterema siłami skupionymi

Przyjęto: beton klasy 8 150 o #*=85 kG/cm², #>.=7,5 kG/cm², £*=230 000 kG/cm², stal klasy A-O o znaku SiOS i #*= #_Bf=1900 kG/cm², 6=70 cm, 6_Ł=210 era, di_r=35 cm, A=90 cm.

Do obliczeń momentu bezwładności przekroju przyjęto:

</' 35    _

4Ł-20+ 30 0,5= 35 cm, -r*^⁰*³⁹*

h 90

b 10    2I0'90**0,535 ■____ *

— — 0,353,    --—^:—=6825263 cm*,

270 ’    ’    12

^z rys. na str. 502 odczytano g=>0,535,

Lm 4

V230QQ0'68_i^,_t/3- _8W9,_{235 cffl}

210*8,5

Tflfoefc* 3-4    \

Obliczenia współczynników rj dla p. A

<(*> V	X	- 1	Si 1	ł» 1	* l	'V*;
Art |	B’2,35 4	2^5	0.715	0.6548	-0.0141 1	0,3238
A-3	n-3,35	2*35	1370	03094	-0,2076 1	-0.0088
	2 1.50	2^5	0,638	0,7590	I 0,1121	0,4260
A-Tf A-iir	4,50	235	1,919	0,0902	— 0,1881	- 0,0494
	10,50	235	4.461	03145	0.0082	-0,0030
A-rv	13.50	2.35	5,745	0.0011	0,0044	0,0028
a~s\	n-2,35	2.35	7,168	0	.0	0
A-4	n-2.35 15+ ■	235	I' ’ 7333	0	1 ^0	°
	2

Korzystając z symetrii wystarczy rozwiązać dwa równania warunkowe: M_A=0, Q_A= 0 wg wzoru -0,2076*1+0,1121*80,0-0,1888*120,0+0,0082-120.0+0,0044-80,0=0,

—0,3238*i+0,4260* 80*0—0,0494* 120,0-0,0030* 120,0+0,0028* 80,0=0,

—0,20761k = +12,352, *,=**=-59,499 T,

-0,3238*i= -28,016, *, = *₃= +86,523 T.

Obliczenie momentów w przekrojach I, II, C, D wg wzoru

i l ~ m=—YPi**

a) Dla przekroju I (rys 3.38)

Tabela 3.5

Obliczenie współczynników tj dla p. /

■ SM: y	X, _	L	, '*$■ 1	łi	Óa	Ii
I-I	n-2,35 Pi 4	. 2.35	1,423	0.2749	-00021 1	0.0359
1-2	ggjg	2,35	2,208	0,0234 1	-0,1538 1	-0,0650
M ,	0 ;	2,35	0,00	1,0000	1,0000	1.0000
I-II	3»ó	2,35	1377	0.3639	-0.1846	0,0821
i-m	9,0	2,35	3,830	-0,0306	-0,0031	-0,0t68
(-IV	12.0	2,35	5,106	-0,0032	0,0080	0,0023
W	**2,35 13,5+ 4	2,35	6,530	0i0012	0.0012	0,0015
1-4	n-2,35 13,5+——— 2	2,35	7,315	0	0 .	°

[86,523(—0,202] ) + (-S9,499)(-0,1538)+80,0-1,0000+ 120,0(—0,1846) +

+120,0(-0,0031)+80,0- 0,0080]- 29,246 Tm .