PA274982

ANALIZA STATYSTYCZNA DANYCH

Testt dla prób zależnych z wykorzystaniem SPSS

Mamy wyniki z dwóch prób zależnych; te same osoby uczestniczyły w obu no ■ rach. Wobec tego potrzebne nam są dwie zmienne: jedna dla wyników z pienJ* go pomiaru „risza”, druga - dla drugiego pomiaru „hałas”. Należy pamiętaj jl wyniki danej osoby byty w tym samym wierszu (dane; Rozdńal3J>.suv).

W górnym menu wybieramy opcję ANALIZA, potem PORÓWNYWMii, stępnie TEST T DLA PRÓB ZALEŻNYCH, po czym pojawji

ŚREDNICH, a następnie

okno TEST T DLA PRÓB ZALEŻNYCH (rys. 8.7).

Aneka Wytowy Narzędzia 1 Raporty warstwowe 0p« Matydyczrty

Ogćty mooei kwoty Modtfemnzane Koełacje ' '

Regresja

klasyfikacja | fi«*Jcqa danych Skalowane

Ttafy nieparametryczne AnaSzy przeżycia Weiokrotne odDowieda

Średnie

Test Łdk jednej próby .. i Test t da prób niezależnych .

> Jeohoczyrnkowa ANOVA..

Rys. 8.7. Wybór TESTU T DLA PRÓB ZALEŻNYCH z górnego menu.

W oknie TEST T DLA PRÓB ZALEŻNYCH, w polu po lewej stronic mamy, jak zwykle, wszystkie zmienne, jakie wprowadzone zostały do Edytora danych (rys. 8.8). Teraz musimy wybrać parę pomiarów, które chcemy ze sobą porównać (rys. 8.9). Aby to zrobić, trzeba najpierw kliknąć nazwę jednej zmiennej, która zostanie wpisana w miejsce AKTUALNY WYBÓR ZMIENNA 1, a następnie nazw drugiej zmiennej, która też znajdzie się w części AKTUALNY WYBÓR. Dopiero po pojawieniu się obu zmiennych w częśri AKTUALNY WYBÓR, przenosimy zaznaczoną parę w pole PARY ZMIENNYCH korzystając z przydsku 33 (rys. 8i).

i

m

Resetujj AnuM | . Pomoc |

Afcfoafry wyto

: Ziwerwel deć

a ZaiennaZ hakat

Ot***- 1

Rys. 8.8. Definicja zmiennych w oknie TESTU T DLA PRÓB ZALEŻNYCH.

8 • PORÓWNYWANIE DWÓCH GRUP: TESTY T-STUDENTA...

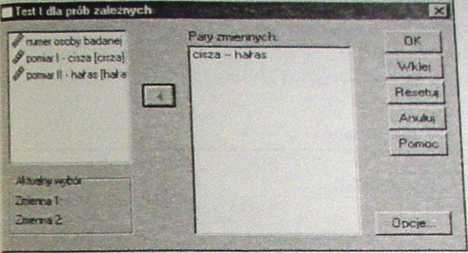
Rys. 8.9. Zdefiniowana para zmiennych w oknie TESTU T DLA PRÓB ZALEŻNYCH.

Na koniec klikamy OK, po czym automatycznie pojawia się Edytor raportów.

W Edytorze raportów zamieszczone są trzy tabele. Z pierwszej tabeli STATYSTYKI DLA PRÓB ZALEŻNYCH (rys. 8.10) odczytujemy statystyki opisowe: średnie wyników oraz odchylenia standardowe dla pomiaru pierwszego „cisza” (M = 14,75; SD = 4,60) i pomiaru drugiego „hałas” (M = 11,55; SD = 4,23).

Statystyki da prób zależnych

	Średnia	N	Odchylenie standardowe	Błąd standardowy średnie!
Para pomiar I - ctsza	14.7500	20	4.59834	1,02822
^1 pomiar U-hałas	11,5500	20	4,23612	,94723

Rys. 8.10. Statystyki opisowe.

W drugiej tabeli KORELACJA DLA PRÓB ZALEŻNYCH (rys. 8.11) uzyskujemy informację na temat poziomu skorelowana wyników pochodzących z obu pomiarów. W prezentowanym przykładzie wvniki są silnie skorelowane (r = 0,72;

P < 0,001).

Korelacje da prób zależnych

	N	Korelacja | Istotność
Para pomiar i - cisza & i pomiar ł! - hałas	20	.721	.000

Rys. 8.11. Współczynnik korelacji r-Pearsona.

Wreszcie, w trzeciej tabeli TEST DLA PRÓB ZALEŻNYCH (rys. 8.12), znajdujemy w pierwszej kolejności informacje dotyczące wielkości różnicy między wynikami z pierwszego i drugiego pomiaru (średnia różnic, odchylenie standardowe tych różnic). Średnia różnic i odchylenie standardowe różnic będą przydatne do obliczenia miary wielkości efektu, ale o tym nieco później. Tymczasem sprawdzamy dane konieczne do podjęcia decyzji o odrzuceniu hipotezy zerowej. Odrzucamy hipotezę zerową na rzecz hipotezy alternatywnej i stwierdzamy, że poprawność wyko-