PC043348

/

J. fWlłiJt ftitfwj :mlrnn*J

frtykktd 3.9.

I) WykiłA*inv. mi cmi a* * *1,«i N, Jm nubtolny ilu « Ko/wiąmiii mow •I > 9 jo*t. w ufiMnym pr/yptulku, trudne. NitleZy jednak uuwiM, tfwtnhHiN. jelit #i • # + I, Wyntarciy wlfc przyjąć jV. ■ / ♦ I i warunek o ,' tpetnluny

h) Urflilieij ciągu </„ - /i'    2n, m JV, Jwt «o. tratwo to rauwalyć, pnrtioa.

wyrazy cliyiu ilu pontaci //„ » n\ I * ( Rozwalania u.* nlttrudin przypadek ciągu

lidzie I t IV, i*o.....ui sij danymi lic/hnnii, o* / O. Oranlci| ciągu («„) jm „..

-w», Jiiohownie do tego czy o* > O, czy nt < 0.

iwicni/ęiiic ,1.2 moźnu uogólnić nu przypadek granic niewłaściwych, kładowo, josli o„ -* iw, b„ > c ■ A*. to («_/( + b_n) —* oo, b„/o„ —* O, a_nb_n »»*,, ile c > O, nutomiuNt <i_nb_H —* —oo wówczas, gdy c < 0. Nic będziemy tu pr/ju azali wszystkich tego typu stwlerdzcri. Kłopoty pojawiąją się w przypadku tu wyrażeń nieoznaczonych, np. jeśli jeden z ciągów (c/„), (b_H) dąży do oo, ndn. do -<», to bez dodnlkowych Informacji nie można wiele powiedzieć o gnui ciągu (o„ + b,,) (może ono nawet w ogóle nie istnieć). Jest to przykład tzw.iy mżenia nieoznaczonego typu oo — oo (symbol oo — oo nie jest zapisem dziali* arytmetycznego, lecz jedynie umownym znakiem, który oznacza typ wynfc nia nieoznaczonego), Innymi wyrażeniami nieoznaczonymi są: jj, 0-w,l‘, oo° itp. Obliczenie granicy w takim przypudku jest zwykle trudne i najcz^ck) jest poprzedzone stosownymi przekształceniami. Niektóre z nich pokaztlifaj w przykładzie 3.5.

twierdzenie o trzech ciągach jest prawdziwe także w przypadku granic ns właściwych, W takiej sytuacji problem nieco się upraszcza w tym sensie,ii wystarczy jedno oszacowanie dla wyrazów ciągu zamiast dwóch, jak miało a miejsce w twierdzeniu 3.4(a). Jeśli pokażemy, że a„ > b„ dla każdegon lew (bn) mu granicę oo, to taką samą granicę ma ciąg (o,,). Jeśli a„ < b_n i (ł»,) dąb do -oo, to ciąg (o,,) także dąży do tej granicy.

Kolejne twierdzenie jest prostym wnioskiem z twierdzenia o trzech clągad Twikrokgnik 3.7.

Załóżmy, że «„ ^ O dla n e A⁷ i istnieje granica

lim

Jeśli u < 1, to lim «>, » 0. Jeśli ą > 1, to lim |o„| = oo.

Jeżeli dla ciągu («„) istnieje granica lim = r, to lim a„ = 0. o ue r

oraz lim la.l * oo, o ile r > 1.

II

3.1. Clttfl llcthowr

1'rzyktml 3.10.

Obliczymy granicę eli||| „_H •    . » < N Sknnyilamy / <wuinlcgi> twierdzenia. W r

wołanym przypadku mamy

<i

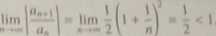
Granico ciągu (u„) Jest więc równo O, Mówimy, ge ciąg (2") dęły do nlcsknóeMtnnfct iz.ybcle) niż ciąg (w*), Łotwo uogólnić uzyskany wynik: dla dowolnych o • R, h » l ciąg (p) dąży do 0.

Dla dowolnego e c R clęg (4) dąży do 0. RzeczywMcic, granica z twierdzenia 3.7 jest równa

Twierdzenie 3.8. Ciąg

Jest rosnący I ograniczony, a więc zbieżny.

Uwaga. Granicę (3.5) nazywumy stułą Eulera I oznaczamy symbolem c. Jest lo liczba niewymierna, której przybliżona wartość jest równa 2,71828,.. Obok liczby /r, jest nąjważniejszą stałą w matematyce. Odgrywa szczególną rolę w matematyce finansowej i ekonomii.

Przykład 3.11.

Obliczymy granicę ciągu

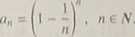
Proste przekształcenia prowadzą do wniosku, iż dla n > 1 mamy

Mianownik dąży do e • 1, licznik do I - rozważany ciąg ma więc granicę e~^ł.

Niebanalnym do wykazania uogólnieniem ostatniego przykładu Jest kolejne twierdzenie.

Twierdzenie 3.9.

Dla każdego x € R mamy

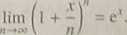
w* nimf, w_

107