14367 PC043365

V2 ,W2. 1

jr³(ar+ 1>

X3(X -ł- 1)

dx = 2lnx-2x~ⁱ + x~² -21a(x +1) + c.

Rozdział 3.	Funkcje jednej zmiennej
na ułamki proste	kilku funkcji wymiernych:
2x — 1	A B
-r^2-!	x — 1 X +1 ’
*-l	Ax + B C D
(X^2 + IX*^2 - 2)	*^2+i x-v5 x + v5’
40 - 2	AB C D
x?(x +1)	X X^2 X^3 X+l

Sprowadzając wyrażenia po prawych stronach do wspólnego mianownika i porównują współczynniki przy jednakowych potęgach x, łatwo wyznaczyć wartości stałych. Zatem

x - 1 x + 1 ’

-W 11111

C*»+iX**-2)    *² + i ⁺ _X-V5 ⁺ pif ’

4x²-2    2    2    -2    -2

x+\

= - + Hr + -^ +

Przykład 3.58.

Obliczymy całki funkcji wymiernych z przykładu 3.57. Z twierdzenia 3.44 wynih, że całkowanie funkcji wymiernych sprowadza się do całkowania ułamków prostych. Całkujemy kolejne ułamki proste, otrzymując:

2x-l 1, B §    3

_xi__J d* = — ln(jr — 1) + — ln(jc + l)+c,

Na zakończenie zauważmy, że niektóre całki zawierające funkcje trygonometryczne można obliczyć, korzystając z podstawienia t = tg(f). Wówczas

21

1 + f²’

1-r² _J f 2 dr

COSJC = --r, dx =

1 +r²’

K

(327)

Przykład 3.59. Całkę

1 = f — óx J cos*

łatwo wyznaczyć za pomocą podstawienia (3.27):

l+tg|

' i f-rh** f(rr, | rb)*'-'"¹¹ -^{,l+to11+,|+c=,n}

W poprzednich podrozdziałach była mowa o tym, że funkcje elementarne $ą różniczkowalne, a ich pochodne są także funkcjami elementarnymi. Inaczej jest przy całkowaniu.

Istnieją takie funkcje elementarne, których całki nie wyrażają się w postaci funkcji elementarnych. Przykładami tego typu całek są:

Należy w tym miejscu wyraźnie stwierdzić, że całki powyższe są pewnymi funkcjami, tyle tylko, że nienależącymi do rodziny funkcji elementarnych.

3ii. Całka oznaczona

Niech /: (a,b) —» R będzie funkcją ograniczoną. Rozważmy dowolny ciąg .yoiJti,..., x„ spełniający warunek

a = xq < jci < xz < •. - < x_n = b.

Punkty te wyznaczają podział <xq,xi>, <xj,X2>, ...<x«_i,x„> przedziału (a,b). W każdym z tych przedziałów wybierzmy po jednej liczbie ej, .... c„. Dla każdego podziału P i układu liczb c = (ci.....c„) wyznaczmy sumę

n

i=i

(3.28)

zwaną sumą całkową. Liczbę ó(P) = max,-(x,- - x,_i) nazywamy średnicą podziału P.

Definicja 3.24.

Niech a, b, gdzie a < b będą ustalonymi liczbami.

Mówimy, że ograniczona funkcja/: {a,b) —* R jest całkowalna (wsensie Riemanna) wtedy i tylko wtedy, gdy istnieje liczba

(3.29)

lim S(f, P, ć)

ó(P)->0

i jej wartość nie zależy od podziału P oraz od wybranych punktów, tj. c.

Granicę tę nazywamy całką funkcji / na przedziale (a, b) i oznaczamy symbolem

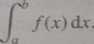
(3.30)

Liczby a i b nazywamy, odpowiednio, dolną i górną granicą całkowania.

141