s 203

203

7.3. Przyspieszenie punktów ciała w mchu płaskim

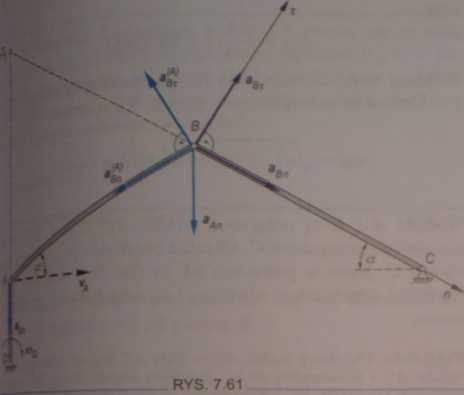
Ob = &Bn + flfii

(2)

gfafefnyspieszenie agn leży na normalnej do toru punktu B i je* równe

BC

ob„ —

co„r

ftnewiż Vg = (oO\B — (Do^r, więc agn = —

Po porównaniu wzorów (1) i (2) dostajemy zależność

(3)

+ O-Bj U «An +    + ^Br I

Z tefo równania wektorowego można uzyskać dwa nie-oieżat równania skalarowe. W tym przypadku jest wygodnie fanie 0) zrzutować na osie n i r, stąd

agii HŁ. cos 60° —    cos 60° — « jjj? cos 30°

M_m( -<Ą,^r MU "oA 1 _ "o^r

Widać stąd, że przyspieszenie styczne a⁽g_r^} ma zwrot prze-fay niż na rys. 7.61.

fcyspieszenie styczne abt będzie równe ^aBt = ^aAn COS 30° — Qg^ COS 30° — cos 30°