s 205

205

7.3. Przyspieszenie punktów ciała w ruchu płaskim

Zadanie 7.47

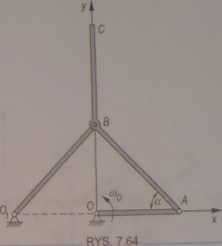
V/ mechanizmie Czebyszewa korba O A obraca się ze stałą p^ftością (Wo. Znaleźć przyspieszenie punktów fi i C w położeniu mechanizmu jak na rys. 7.64, jeżeli O A = r, AB = _s 0\B — r-Jl, BC — 2r, a m 45°. Znaleźć chwilowy środek przyspieszeń łącznika ABC.

Odpowiedź

a_By=0

fla 10, a_Cy m —-a>₀^r

Chwilowy środek^ przyspieszeń leży na kierunku AB V odległości rV2 od punktu fi.

Grupa IV

Do grupy tej zaliczamy wszystkie te zadania, w których mamy dane przyspieszenia dwóch punktów ciała, a należy obliczyć jego prędkość kątową, przyspieszenie kątowe oraz przyspieszenie dowolnego innego punktu.

Trójkąt równoboczny ABC porusza się w płaszczyźnie ry- PRZYKŁAD 7.48 sunku. Przyspieszenia punktów A i fi są skierowane jak na rys. 7.65 i wynoszą a_A = a_B — a. Bok trójkąta jest równy b.

Znaleźć prędkość końcową co, przyspieszenie e oraz przyspieszenie punktu C.

I ROZWIĄZANIE hzyspeszenie punktu fi wynosi

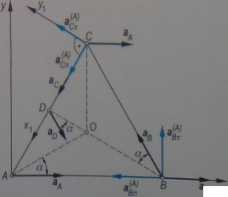
-RYS. 7.65

•a X

M “ ^aA +    = &A + <^_Bx + ^aBn

Rzutując je na osie przyjętego układu współrzędnych, otrzymamy

9 —a_B cos 60° == — stąd

a

P)

Bn

1    3

— a_A + -a_B = -a

Ponieważ

H = o)² AB = co²b