Scan154 (2)

154 B.F. Pennington i R.K. Olson różna. Następnie liczymy analizy regresji do średniej z populacji i porównujemy ich wartość w grupach jedno- i dwujajowych bliźniąt. Wynik każdego z bliźniąt jest najpierw podzielony przez średni wynik drugiego z bliźniąt. W ten sposób, średnie wartości dla osoby z dysleksjąz pary bliźniąt jedno- i dwujajowych wynoszą 1, podczas gdy średnie wartości dla ich współbliźniąt znajdują się gdzieś pomiędzy jedynką a zerem, czyli średniącałej populacji. Aby zrozumieć metodę DF załóżmy, że jedynie czynniki genetyczne mają wpływ na dysleksję, (odzie-dziczalność deficytów grupy (h _g)=l)oraz,żeniewystępujetubłądtestu. W takim wypadku jednojajowi współbliźniacy osób z dysleksją nie powinni wykazywać regresji do średniej dla populacji (powinni oni wykazywać dokładnie takie samo natężenie deficytu jak ich dyslektyczni współbliźniacy), podczas gdy współbliźniacy dwujajowi powinni wykazywać regresję połowiczą w kierunku średniej dla populacji, ponieważ bliźnięta dwujajowe mają wspólną średnio połowę genów segregacyjnych (patrz Ryc. la, przedstawiająca graficznie taki hipotetyczny wynik. Należy zauważyć, że h _g jest równe podwójnej

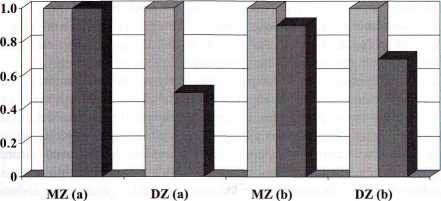
H Średnie dla tego z bliźniąt, który przejawia określoną cechę I Średnie dla współbliźniąt

Ryc. 1. (a) Regresja do średniej w populacji oszacowana dla współbliźniąt MZ i DZ, przy założeniu, że mierzony deficyt grupy wynika wyłącznie z wpływów genetycznych; (b) Regresja do średniej w populacji oszacowana dla współbliźniąt MZ i DZ, przy założeniu, że mierzony deficyt grupy wynika ze specyficznego środowiska (0.1), wpływu genetycznego (0.4) i wspólnego środowiska (0.5)

Genetyka dysleksji 155

wartości różnicy pomiędzy regresją współbliźniąt jedno- i dwujajowych.

k. Oczywiście, nie da się całkowicie uniknąć wystąpienia błędu w teście łub występowania różnic w czynnikach środowiskowych, mających wpływ na pomiary czytania, które spowodują wystąpienie pewnej tegresji w przypadku współbliźniąt j ednoj aj owych. Regresja współbliźniąt jednojajowych do średniej wartości dla populacji jest bezpośrednim sposobem oszacowania wpływu czynników środowiska różnych dla każdego z bliźniąt (e _g) na deficyt grupy, ponieważ bliźnięta jednojajowe mają wspólne zarówno wszystkie geny, jak i środowisk© rodzinne. Na Rycinie lb regresja współbliźniźniąt jednojajowych o 10% do wartości 0.9. oznacza, że e _g wynosi O. 1. Wynika z tego, że 10% deficytu grupy Związana jest z wpływem czynników środowiskowych różnych dla każdego z bliźniąt.

' i Za pomocą analizy DF można również oszacować stopień, w jakim łlfeficyt grupy wynika z czynników środowiskowych wspólnych dla bliźniąt w poszczególnych parach (c g). Załóżmy, że odmienne wpływy środowiskowe sąniewielłde, a współbliźnięta jedno- i dwujajowe wykasują tylko nieznaczną, i na dodatek, bardzo zbliżoną, regresję w kierunku Średniej dla populacji; W takim wypadku, pomimo oczywistych różnic :'f|ś>między bliźniętami MZ i DZ do podobieństwa genetycznego, wpływ wspólnych czynników środowiska na deficyt grupy ocenilibyśmy jako duży, a wpływ genów jako zerowy. Jednak, dla wielu wskaźników behawioralnych najbardziej prawdopodobne jest, że wystąpi pewien ;iwpływ genów, a także wpływ różnego i wspólnego środowiska. ^Hipotetyczny wynik dla regresji współbliźniąt jedno- i dwujajowych zilustrowano naRyc. lb. Pokazuje ona, że średnia wartość dla współbliźniąt jednojajowych wynosi 0.9, zaś średnia wartość dla współbliźniąt dwujajowych wynosi 0.7. DeFries i Fulker (1988) wykazali, że odziedzi-dzalność deficytów grupy równa jest podwójnej różnicy pomiędzy t^ędnimi wąrtościami uzyskanymi przez jednegosz pary bliźniąt j edno- i dwujajowych, po podzieleniu ich wyników przez średnie wartości uzyskane przez ich współbliźniaków. Przykład podany na Ryc. Ib Wskazywałby na odziedziczalność równą (0.9 - 0.7) x 2 = 0.4. Stwierdzono regresję współbliźniąt jednojajowych do wartości 0.9, a więc ie-_g=0.1, a h²e=0.4, e_f = 1 - (0.1 + 0.4)=0.5. Tak, więc, połowa deficytów grupy w tym przykładzie wynikała ze wspólnych wpływów środowisko-