Scan Pic0021

a więc

T = fmg cos a.

II zasada dynamiki przyjmuje w tym wypadku postać:

mg sin a - fmg cos a = ma,

skąd

sin a-a gcosa

Wstawiając a = 30° i a = —g otrzymujemy:

1 _ V3

^/_2V3 " 6 ’

Rozwiązanie zadania 1.39 Prawidłowa odpowiedź: A.

Poruszając się z prędkością v ciało posiada energię kinetyczną

E_k ⁼ —mu². Zgodnie z definicją, energia kinetyczna jest taką wielkością

opisującą stan ciała, że jej zmiana równa jest pracy siły wypadkowej działającej na to ciało:

aą=H

'wypadkowej

Wypadkową siłą działającą na ciało, o którym mowa w zadaniu, jest siła tarcia T (ciężar i siła sprężystości podłoża równoważą się wzajemnie). Tak więc

końcowa ^k początkowa ^ Ar,

gdzie Ar jest wektorem przemieszczenia, którego długość (w ruchu prostoliniowym) jest równa przebytej drodze s. Ponieważ w zadaniu prędkość końcowa ciała jest równa zeru, mamy więc

AE_k = 0-—mvl = Ts cos A.    Ar) = Ts cos 180°=-Ts,

czyli

—muł = Ts.

2 ⁰

Wartość siły tarcia jest równa T = fF_n , gdzie / jest współczynnikiem tarcia, a F_n - wartością siły nacisku ciała na podłoże i na poziomej powierzchni wynosi ona F_n = mg.

Po podstawieniu wyrażenia na siłę tarcia do wyprowadzonego wyżej równania otrzymamy:

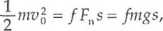
skąd

/ =

2 gs

Rozwiązanie zadania 1.40

Prawidłowa odpowiedź: A.

Podobnie jak w poprzednim zadaniu, dochodzimy do stwierdzenia, że

—mol =Ts, 2 ⁰

gdzie T jest wartością siły oporu i wynosi T = —mg.

Drogę przebytą ruchem jednostaj- y, nie opóźnionym można obliczyć ze wzoru

, 1 ,2 s = vJ—at ⁰ 2

lub jako pole powierzchni figury pod wykresem v(t).

W tym wypadku jest to pole trójkąta

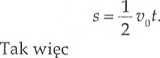
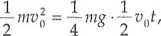
stąd f =

4v,

o

= 3,4 s.

- 41 -