S7300535

Poprawkowe kolokwium zaliczeniowe z przedmiotu „Algebra liniowa¹' WETI, kierunki AiR, EiT i IBM, 1 sem., r. ak. 2010/2011

1. [7p.J Wyznaczyć macierz odwrotną A ¹ (o ile istnieje) do macierzy

2. [7p.] a) Obliczyć det(£ • B^T) dla

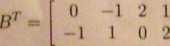
[2p.| b) Podać i zilustrować na przykładach cztery własności wyznaczników.

3. [7p.] a) W zależności od parametru A podać liczbę rozwiązań układu równań

Az ■+■ y + 2 z = 1 z + Ap + 2z = l z + y + 2Az = 1

[2p.) b) Podać po jednym przykładzie macierzy osobliwej trójkątnej górnej i macierzy nieosobliwej diagonalnej stopnia co najmniej trzeciego.

4. [7p.| Znaleźć równanie płaszczyzny n przechodzącej przez początek układu współrzędnych i prostopadłej do dwóch płaszczyzn iri : 2x — y + 5z - 3 = 0 i zra: z + 3y - z - 7 = 0.

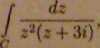
6. [7p.] a) Znaleźć oryginał, gdy dana jest transformata Laplace’a

F(t) -    ¹³"-tl⁶—

^w a³ + 4s³ + 13s

[2p.] b) Wyprowadzić wzór na transformatę Laplaco*a oryginału f(t) — e*.

7. *) [dla chętnych] [5p.J Dane są wektory S *» [3, —2,1], b ** [1,2,1], c =* (—1,4.3). Obliczyć

[(6 o Ć)(2ćT x 5)] o [(£ - S) x (S + Ć)J.