068 069

68 Eliza Mytych. Ludwik Kumański

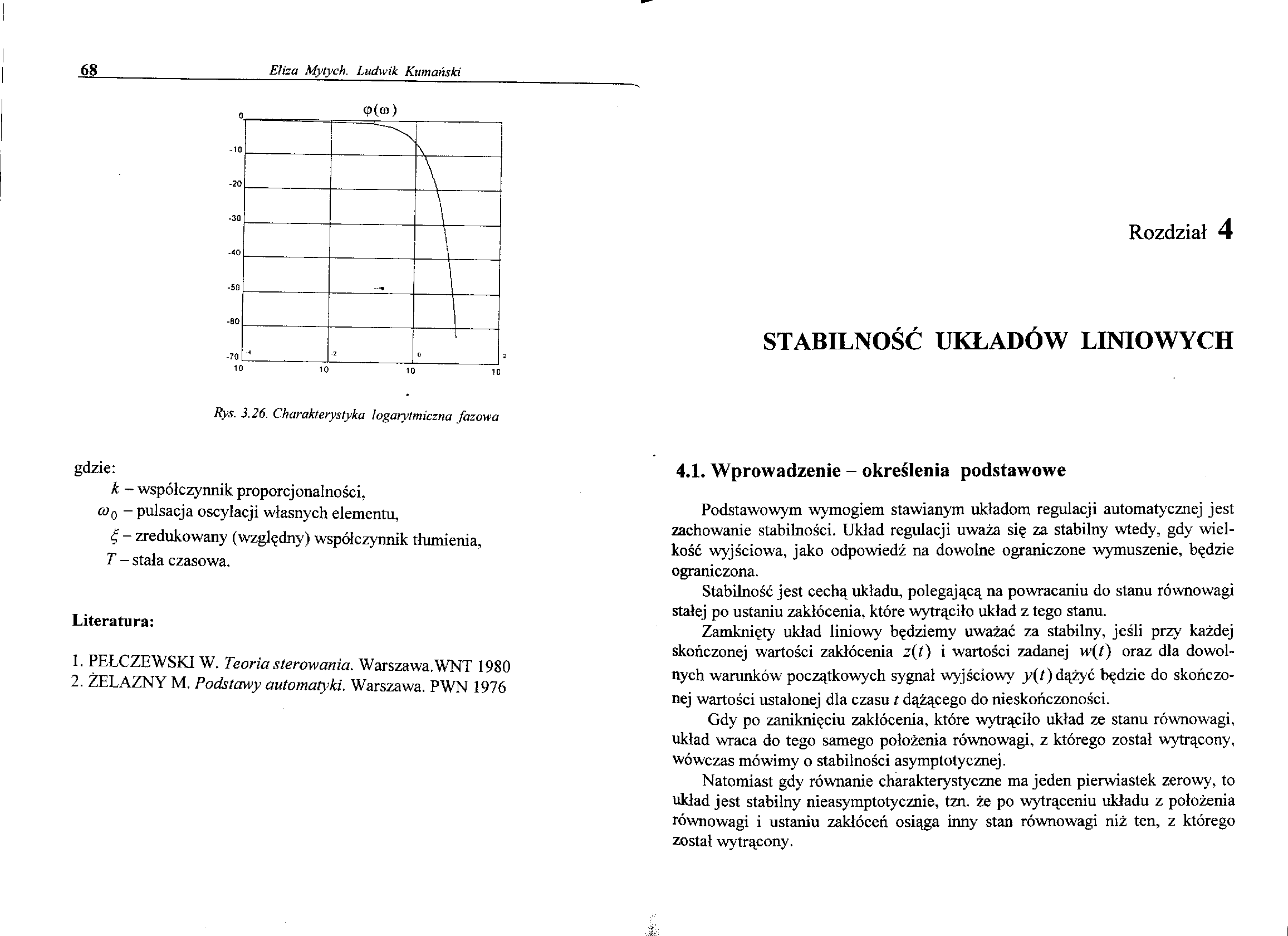
Rys. 3.26. Charakterystyka logarytmiczna fazowa

gdzie:

k ~ współczynnik proporcjonalności,

(oo - pulsacja oscylacji własnych elementu,

£ - zredukowany (względny) współczynnik tłumienia, T - stała czasowa.

Literatura:

1.    PEŁCZEWSKI W. Teoria sterowania. Warszawa. WNT 1980

2.    ŻELAZNY M. Podstawy automatyki. Warszawa. PWN 1976

Rozdział 4

STABILNOŚĆ UKŁADÓW LINIOWYCH

4.1. Wprowadzenie - określenia podstawowe

Podstawowym wymogiem stawianym układom regulacji automatycznej jest zachowanie stabilności. Układ regulacji uważa się za stabilny wtedy, gdy wielkość wyjściowa, jako odpowiedź na dowolne ograniczone wymuszenie, będzie ograniczona.

Stabilność jest cechą układu, polegającą na powracaniu do stanu równowagi stałej po ustaniu zakłócenia, które wytrąciło układ z tego stanu.

Zamknięty układ liniowy będziemy uważać za stabilny, jeśli przy każdej skończonej wartości zakłócenia z(t) i wartości zadanej w(7) oraz dla dowolnych warunków początkowych sygnał wyjściowy y(/) dążyć będzie do skończonej wartości ustalonej dla czasu t dążącego do nieskończoności.

Gdy po zaniknięciu zakłócenia, które wytrąciło układ ze stanu równowagi, układ wraca do tego samego położenia równowagi, z którego został wytrącony, wówczas mówimy o stabilności asymptotycznej.

Natomiast gdy równanie charakterystyczne ma jeden pierwiastek zerowy, to układ jest stabilny nieasymptotycznie, tzn. że po wytrąceniu układu z położenia równowagi i ustaniu zakłóceń osiąga inny stan równowagi niż ten, z którego został wytrącony.