206 207

204

204

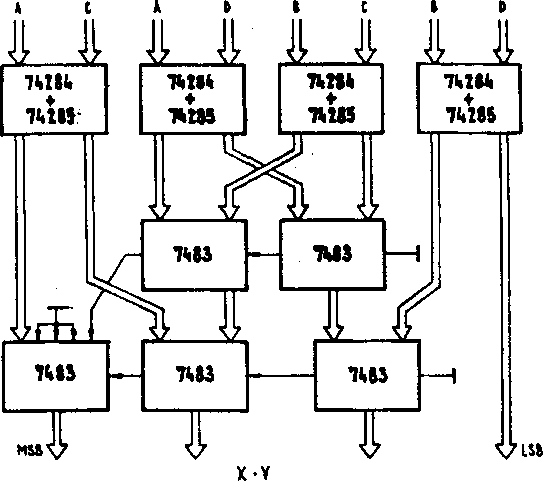
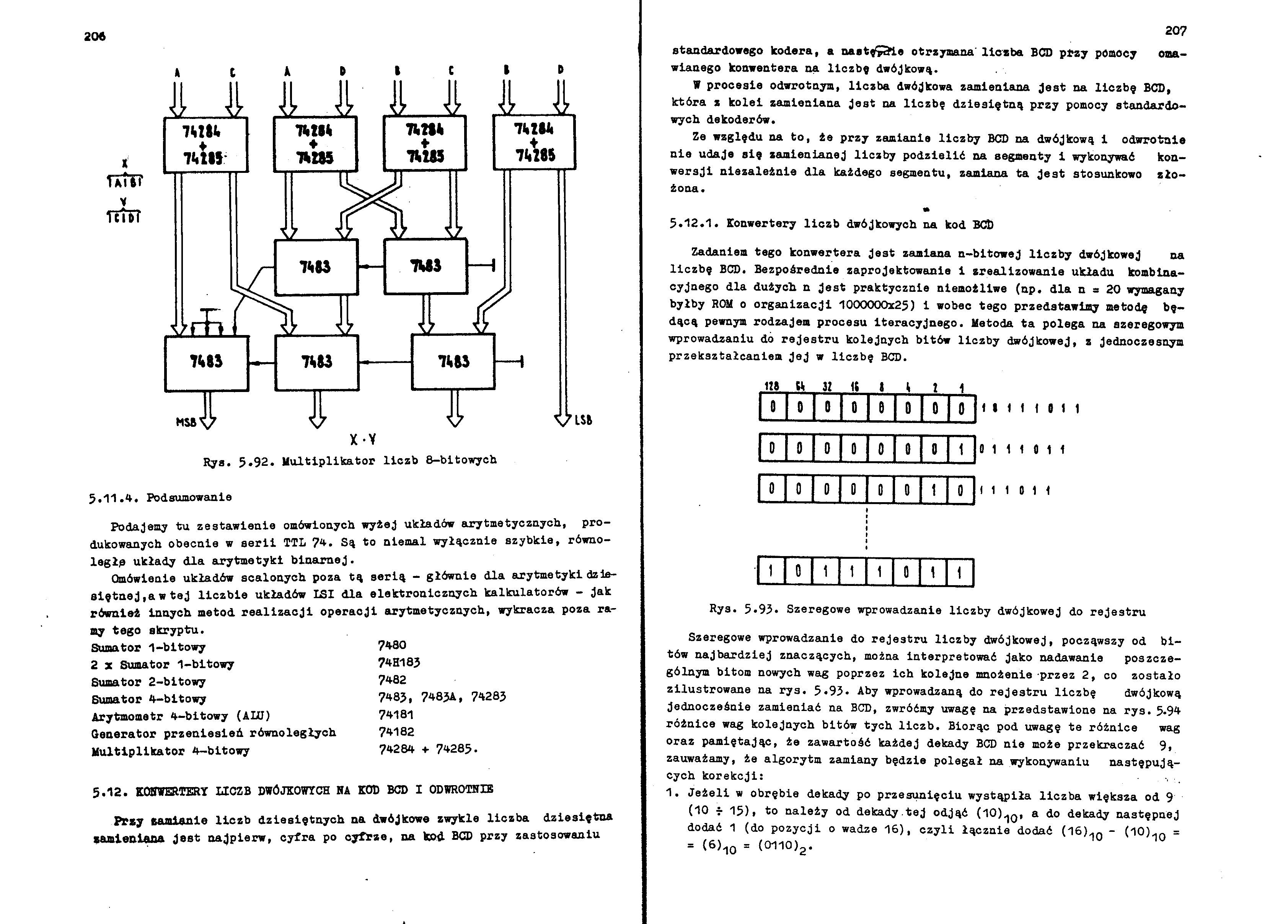
Bya. 5.92. Multiplikator liczb 8-bitowych

l

TTiTf

TefóT

5.11.4. Podsumowanie

Podajemy tu zestawienie omówionych wyżej układów arytmetycznych, produkowanych obecnie w serii TTL ?4. Są to niemal wyłącznie szybkie, równoległo układy dla arytmetyki binarnej.

Omówienie układów scalonych poza tą serią - głównie dla arytmetyki dziesiętnej ,a w tej liczbie układów ISI dla elektronicznych kalkulatorów - jak również Innych metod realizacji operaojl arytmetycznych, wykracza poza ramy tego skryptu.

7480

74H183

7482

7483, 7483A, 74283

74181

74182

74284 + 74285.

Sumator 1-bltowy 2 x Sumator 1-bitowy Sumator 2-bitowy Sumator 4-bltowy Arytmometr 4-bitowy (AHJ)

Generator przeniesień równoległych Multiplikator 4-bitowy

5.12. KONWERTERY LICZB DWÓJKOWYCH HA KOD BCD I ODWROTNIE

Przy zamianie liczb dziesiętnych na dwójkowe zwykle liczba dziesiętna zamieniana jest najpierw, cyfra po cyffcze, na kod BCD przy zastosowaniu standardowego kodera, a nastęędle otrzymana liczba BCD przy pomocy omawianego konwentem na liczbo dwójkową.

V procesie odwrotnym, liczba dwójkowa zamieniana Jest na liczbę BCD, która z kolei zamieniana Jest na liczbę dziesiętną przy pomocy standardowych dekoderów.

Ze względu na to, te przy zamianie liczby BCD na dwójkową 1 odwrotnie nie udaje się zamienianej liczby podzielić na segmenty i wykonywać konwersji niezależnie dla każdego segmentu, zamiana ta Jest stosunkowa złożona.

5.12.1. Konwertery liczb dwójkowych na kod BCD

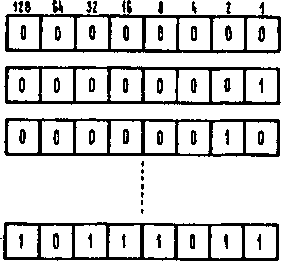
Zadaniem tego konwertera Jest zamiana n-bltowej liczby dwójkowej na liczbę BCD. Bezpośrednie zaprojektowanie 1 zrealizowanie układu komblna-cyjnego dla dużych n Jest praktycznie niemożliwe (np. dla n = 20 wymagany byłby ROM o organizacji 1000000x25) 1 wobec tego przedstawimy metodę będącą pewnym rodzajem procesu iteracyjnego. Metoda ta polega na szeregowym wprowadzaniu dó rejestru kolejnych bitów liczby dwójkowej, z Jednoczesnym przekształcaniem jej w liczbę BCD.

1 I 0 1 1 10 11 0 1 1

Rys. 5.95. Szeregowe wprowadzanie liczby dwójkowej do rejestru

Szeregowe wprowadzanie do rejestru liozby dwójkowej, począwszy od bitów najbardziej znaczących, można interpretować Jako nadawanie poszczególnym bitom nowych wag poprzez ich kolejne mnożenie przez 2, co zostało zilustrowane na rys. 5.93. Aby wprowadzaną do rejestru liczbę dwójkową Jednocześnie zamieniać na BCD, zwróćmy uwagę na przodstawione na rys. 5.94 różnice wag kolejnych bitów tych liczb. Biorąc pod uwagę te różnice wag oraz pamiętając, że zawartość każdej dekady BCD nie może przekraczać 9, zauważamy, że algorytm zamiany będzie polegał na wykonywaniu następujących korekcji:

1. Jeżeli w obrębie dekady po przesunięciu wystąpiła liczba większa od 9 (10 * 15), to należy od dekady.tej odjąć (10)_1Q, a do dekady następnej dodać 1 (do pozycji o wadze 16), czyli łącznie dodać (16),^ - (10)-|o ⁼ = (6)₁₀ = (0110)₂.