23986 spektroskopia034

68

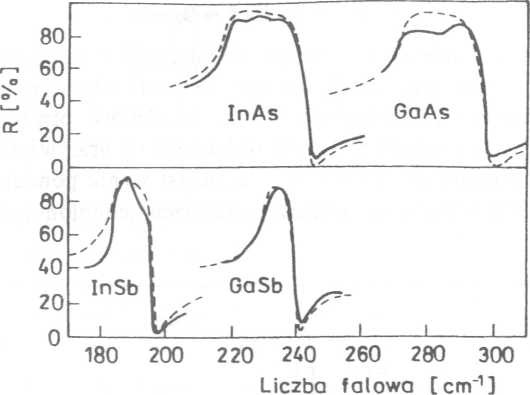
Rys. 35. Widma odbicia sieciowego dla niektórych związków HI —V. Linia ciągła — wyniki pomiarów. Linia przerywana — widma obliczone wg wzorów (7.3), (7.4) [17]

kilku półprzewodników przedstawiono na rys. 35. Absorpcja odpowiadająca widmom przedstawionym na tych rysunkach odpowiada wartościom a > 10⁴ cm^-1.

Jeżeli w komórce elementarnej znajdują się więcej niż 2 atomy, to w zmierzonym widmie odbicia zaobserwujemy więcej niż jedno maksimum. W takim przypadku do analizy trzeba zastosować model

wielooscylatorowy

8

^£0O + X J

oj — co² + Jcoy/

(7.8)

gdzie:    jj — siła oscylatora, częstość rezonansowa i stała tłumienia

dla j-tego oscylatora.

Siła oscylatora wiąże statyczną i wysokoczęstotliwościową stałą dielektryczną następująco:

^(ą-¹)'    ⁽⁷⁹⁾

Dla modelu wielooscylatorowego (7.8) maksima funkcji e₂(co) odpowiadają częstościom fononów poprzecznych co_ro , a maksima funkcji strat Im(— l/s(fu)) dają częstość co_LOj.

Absorpcja wielofononowa

Wielofononowe procesy absorpcji światła są możliwe dzięki oddziaływaniu między fononami, wynikającemu z anharmonizmu drgań. W przybliżeniu harmonicznym fonony są od siebie niezależne i nie oddziałują ze sobą.

Dla absorpcji dwufononowej zasady zachowania mają postać:

hco = hco_l±hco₂,

q = K₁ + K₂.    (7.10)

Znak „+” oznacza sumę, czyli powstanie dwóch fononów, znak ” oznacza różnicę, tj. powstaje jeden fonon, a drugi znika, co odpowiada częstości fotonu, q — wektor falowy fotonu. Ponieważ wektor falowy fotonu można zaniedbać, warunek (7.10) przyjmuje postać

K_x = TK₂.    (7.11)

W absorpcji dwufononowej biorą udział fonony z całej sfery Brillouina, w tym również akustyczne.

Widmo absorpcji jest określone gęstością stanów dwufononowych

~ j|P_iK(K)+<D₂(-K)]|’    ^<7'¹²⁾

gdzie powierzchnia całkowania jest wyznaczona przez warunek

Q)₁(K)+m₂(-K) = m.    (7.13)

Analogicznie do przypadku stanów elektronowych, zerowanie się mianownika w wyrażeniu (7.12) daje punkty krytyczne gęstości stanów.

W odróżnieniu od procesów jednofononowych, absorpcja wielofononowa jest silnie zależna od temperatury. Funkcja rozkładu fononów ma postać

„, = (**!/«•_i)-i, E_l = ha>_i(K),    (7.14)

E_t — energia fononu, n, wyraża liczbę fononów o energii Dla procesów sumacyjnych

E = E_t + E₂, n=l + n₁ + n₂,